Let us consider the four-momentum of a relativistic particle. The temporal component is the energy of the particle. Thus, we can write which is usually referred to as the energy-momentum vector. Since the invariant mass is positive, the energy-momentum vector is time-like and satisfies the mass-shell equation:
Fundamentals of Time and Relativity
Invariant mass
- In relativity, inertial mass and invariant mass are only different in so far that the invariant mass is tied to a specific frame, the rest frame of a particle.
- The four-vector formulation of relativistic mechanics allows to include zero-mass particles (e.g., photons).
8.13
This implies the relativistic energy-momentum relation
8.14
For zero-mass particles the energy-momentum vector is a null vector and equation (8.13) gives . Such particles move at the speed of light , as may be inferred from the general expression for the particle velocity .
The four-momentum is a vector in Minkowski space tangent to the worldline under consideration. We can picture this four-momentum as a vector in the tangent space, i.e., a Minkowski space with its origin at the spacetime point . The orientation of the orthonormal basis in this tangent space can be freely chosen, but two choices are rather natural: (i) alignment with the base vectors of the Minkowski space of spacetime points (observer frame), (ii) alignment of with the tangent to the worldline at (co-moving frame). This is illustrated in the Minkowski diagram below.
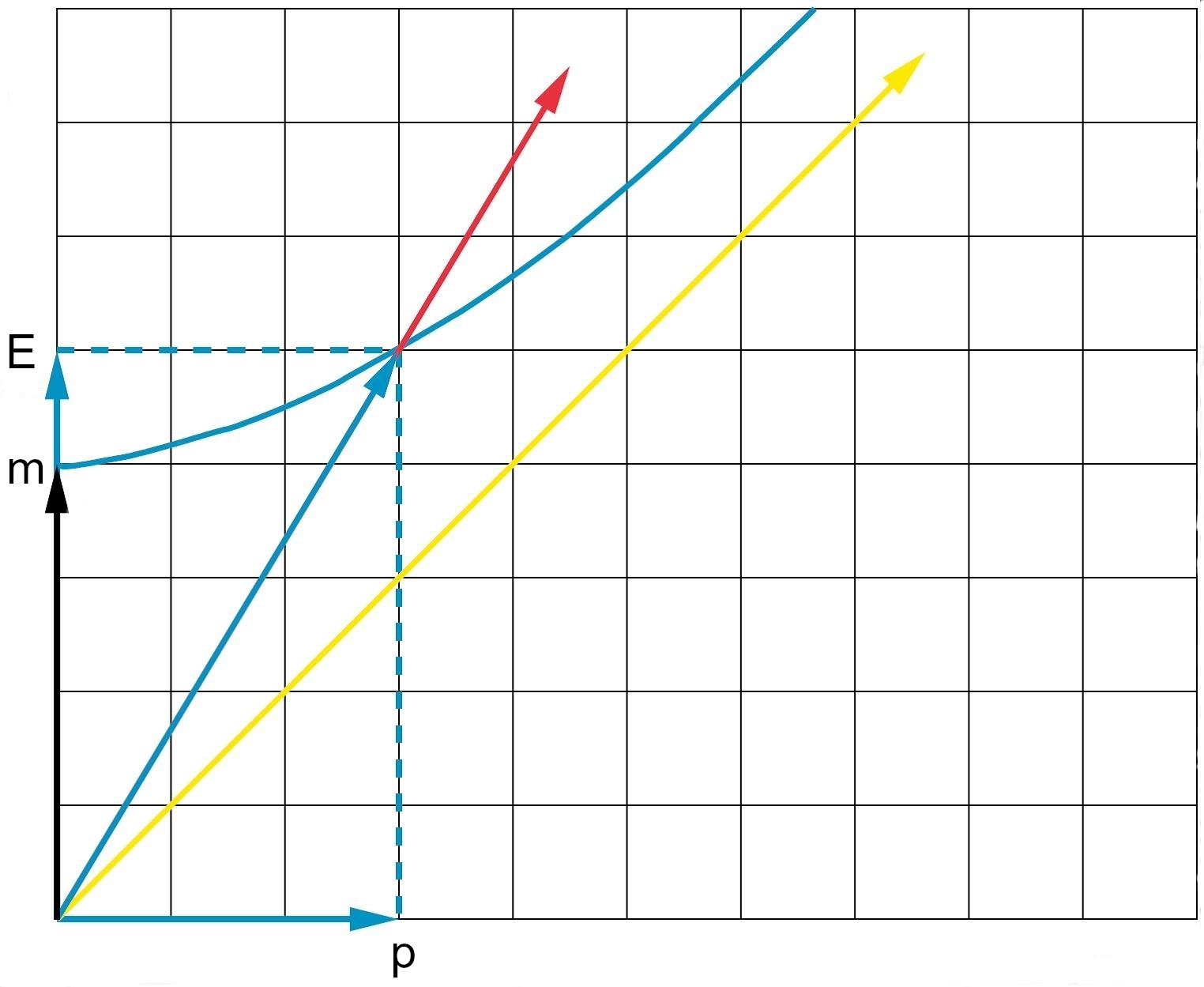
Fig. 8.2 clarifies the relation between energy (inertial mass) and rest energy (invariant mass) of a particle: they are simply related by a Lorentz transformation between the rest frame and an inertial observer frame.
Particle refers here to an idealized model of a quantity of energy that is localized and stable (within some relevant time and energy scale). A composite body, like a proton, a grain of solid or a celestial body, can also be conceptualized as a particle, as long as localization and stability are principal features. The rest mass is then a complex sum of energies of the moving constituent particles, binding energies, energies from internal reaction processes, etc.
- For any fixed value of the invariant mass, energies and momenta related by the mass shell equation (8.13), transform among themselves under rotations and boosts.
- The calculation of the invariant mass of elementary particles from first principles is an ongoing theoretical project.