Consider first the situation of a stationary sphere. Let be the three-vector from the center of the sphere to an inertial receiver at the origin, and let the sphere subtend an angle at the receiver. Photons emitted from the outline of the sphere have frequency four-vectors , with . If a photon appears to the receiver to come from the outline of the sphere, then necessarily satisfies the geometric equation
Fundamentals of Time and Relativity
Moving Sphere
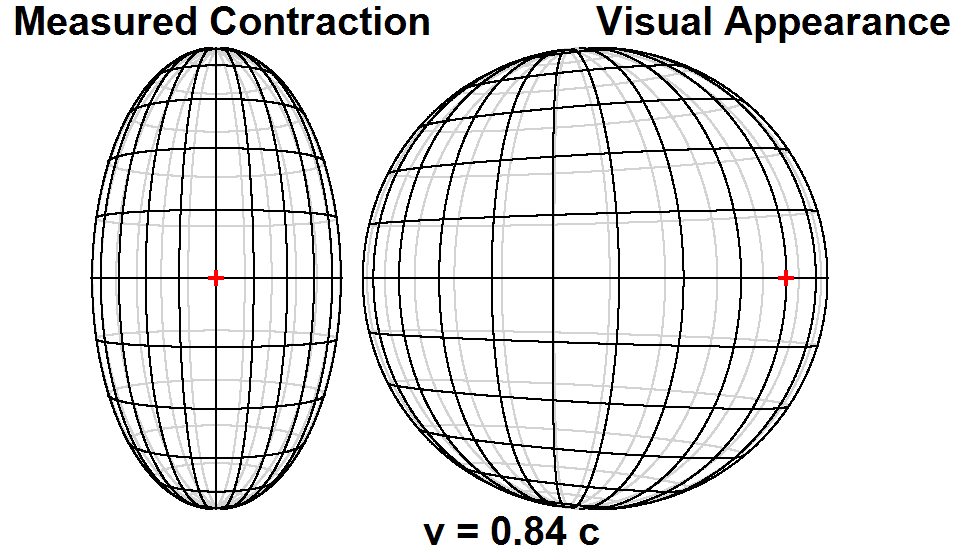
- In 1959 James Terrell and Roger Penrose, independently, pointed out that the visual appearance of a fast-moving object is quite different from its measured shape.
- The visual appearance of a moving sphere is circular, and not contracted along its direction of motion, whatever its speed.
6.6
where is a spacelike four-vector in the receiver’s frame. For the stationary receiver, outline events are characterized by condition (6.6).
To another inertial receiver (e.g., aboard a fast spacecraft), who sees the sphere in the direction , photons arrive from directions . Because the Minkowski product in (6.6) is an invariant, the same condition for outline events holds. Therefore, photons appear to the moving receiver to come from a sphere with outline subtending an angle .
If the second receiver moves with the speed parallel to away from the sphere, we have and . Calculating the ratio from the definition of the four-vector (or by a Lorentz transformation), one obtains the following relation between the subtended angles:
6.7
So as . As the receiver accelerates away from the sphere, the outline grows until it fills the whole sky, apart from a small hole directly ahead.
- To a moving receiver, a sphere still has a circular outline, but of a different size (Penrose, 1959). The sphere is the only geometrical shape that appears the same to all receivers.
- The result (6.7) is just one other form of the relativistic
aberration formula (6.4).