\( \newcommand{\be}{\begin{equation}}
\newcommand{\ee}{\end{equation}} \newcommand{\ba}{\begin{array}}
\newcommand{\ea}{\end{array}} \newcommand{\bea}{\begin{eqnarray}}
\newcommand{\eea}{\end{eqnarray}}
\newcommand{\bean}{\begin{eqnarray*}}
\newcommand{\eean}{\end{eqnarray*}} \newcommand{\la}{\label}
\newcommand{\nn}{\nonumber} \newcommand{\half}{{\scriptstyle
\frac{1}{2}}} \)
The kinetic equation (4.2) becomes meaningful only when the form
of the source term, called the collision integral, has
been established. To obtain an explicit expression we follow a
reasoning originally due to Ludwig Boltzmann, the founder of
kinetic theory (1872).
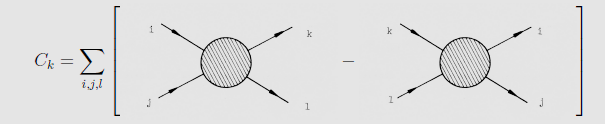
We see from its definition that $C_k$ gives the nett increase of
particles of species $k$ with a given momentum per unit volume and
unit time. Let us denote by $W_{ij|kl}(p_i,p_j|p_i, p_j)$ the
probability that two particles with initial four-momenta $p^\mu
_i, p^\mu _j$ collide and produce two particles with four-momenta
$p^\mu _k, p^\mu _l$ (per unit volume and per unit time). For a
given interaction this rate can be calculated with the aid of
quantum-mechanical scattering theory. In terms of this transition
rate the collision integral looks schematically like
The first term at the right-hand side counts the `gain'
collisions, and the second one the `loss' collisions of particles
with four-momenta $p^\mu _k$.
The transition rate is normalized to two particles per unit
volume. Since the actual number of pairs available is proportional
to the product $f_i f_j$ we have to multiply by this factor. Thus,
the collision term reads more explicitly:
$$ \be C_k[f]=\int \left[f_i
f_j W_{ij|kl}- f_k f_l W_{kl|ij}\right]{\rm{ }}{\rm{,}} \la{4.2}
\ee $$
$$ \be \int := \half \sum
\limits_{l,i,j} \int d{\omega _l}d{\omega _i}d{\omega _j}{\rm{
}}{\rm{.}} \la{4.3} \ee $$
- The integral sign stands for summations and integrations over
all dummy variables. The factor one-half compensates for the
double counting of the two identical states (i,j) and (j,i).
Exercise 3
- Write out the collision integral for a one-component gas.
Indicate explicitly the $x$ and $p$ dependencies of the
various quantities.
The above reasoning is quite general and applies to
non-relativistic as well as relativistic particles, irrespective
of their interaction (barring the long-range Coulomb force). The
specifics of the interaction are hidden in the transition rate.
Because of energy and momentum conservation (4.7) in a collision,
this quantity must contain an four-momentum conserving
delta-function. This guarantees that the two requirements (4.3)
and (4.4) are always identically satisfied.
Moreover $W_{ij|kl}$ can only be different from zero for
collisions in which the appropriate quantum numbers are conserved.
Hence, the collision integral also satisfies requirement (4.6).
Detailed proofs of these statements may be found in the standard
textbooks [2,3,4]
In deriving the Boltzmann collision integral (5.2), we have
overlooked one important aspect, namely, the statistics of the
particles. Suppose the particles are fermions. Then, these
particles cannot scatter into states that are already occupied.
The average occupancy of a one-particle state $k$ is given by
$f_k$. Hence, we must reduce the probability for scattering into
this state by multiplying the transition rate with the so called
blocking factor $1-f_k$ . The collision term which takes
this quantum effect into account was first given by Nordheim
(1928) and Uehling and Uhlenbeck (1933). It has the form [1]:
$$ \be C_k[f]=\int \left[f_i
f_j W_{ij|kl}(1+\et f_k)(1+\et f_l) - f_k f_l W_{kl|ij}(1+\et
f_i)(1+\et f_j)\right]{\rm{ }}{\rm{.}} \la{4.4} \ee $$
- In contrast to fermions, bosons are stimulated to scatter into
states which are already occupied.
- Below we shall see that these additional factors are rather
essential: without them the equilibrium distribution function
would not be a solution of the transport equation.