Reichenbach Coordinates

Einstein time is a special instance, $κ = 1 - 2 ε = 0$ , of the time coordinate $\tilde{t}$ defined in (7.2). Given the facts that secure the consistency conditions of Einstein time, a generalized set of Reichenbach spacetime coordinates ${{\tilde{x}}^{μ}}$ , called a Reichenbach chart, may then consistently be defined. In two dimensions:

This amounts to a synchrony change as depicted in the Minkowski diagram below.

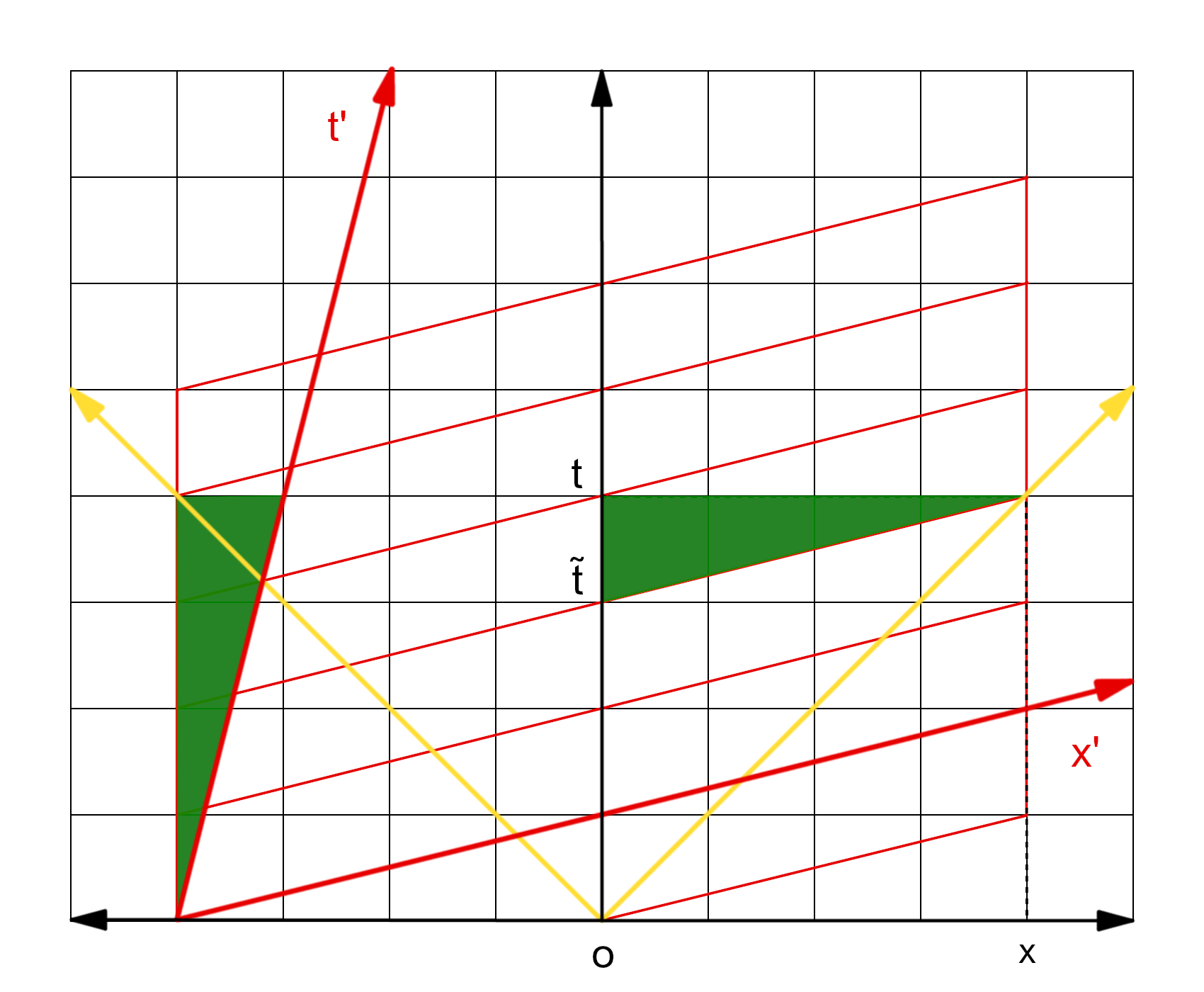
Ruimtetijddiagram — Fig.7.2 Spacetime chart combining the Reichenbach time coordinate $\tilde{t}$ with a Cartesian coordinate $x$ . Reichenbach simultaneity (red lines) is tilted by the angle $\tan α = κ$ marked by the green triangles.

In Fig.7.2 the lines ${t, x; \tilde{t} = const}$ represent sets of Reichenbach simultaneous events. In Minkowski space these sets are flat space-like 3-manifolds, i.e., hyper-planes. Such a family of parallel spacelike hyper-planes corresponds precisely to a particular partition of spacetime into classes of Einstein simultaneous events.

The Reichenbach time coordinate $\tilde{t}$ is identical (up to the scale factor) to the Einstein time coordinate $t^{'}$ adapted to some other inertial frame ${t^{'}, x^{'}}$ moving to the right; see Fig.7.2.

A non-zero value of the arbitrary parameter $κ$ has implications for the symmetry properties of the description. Inertial frames stand out by their symmetry and this gives Einstein simultaneity $κ = 0$ a special status because it leads to global spacetime coordinates that respect the physical symmetries of homogeneity and isotropy.

The Reichenbach chart is just a coordinate change; it does not alter the physics or the predictions of relativity theory in any substantive way.
Reichenbach coordinates do not respect the physical spacetime symmetries, except for the case $κ = 0$ .