Fundamentals of Time and Relativity

Reichenbach Synchronization

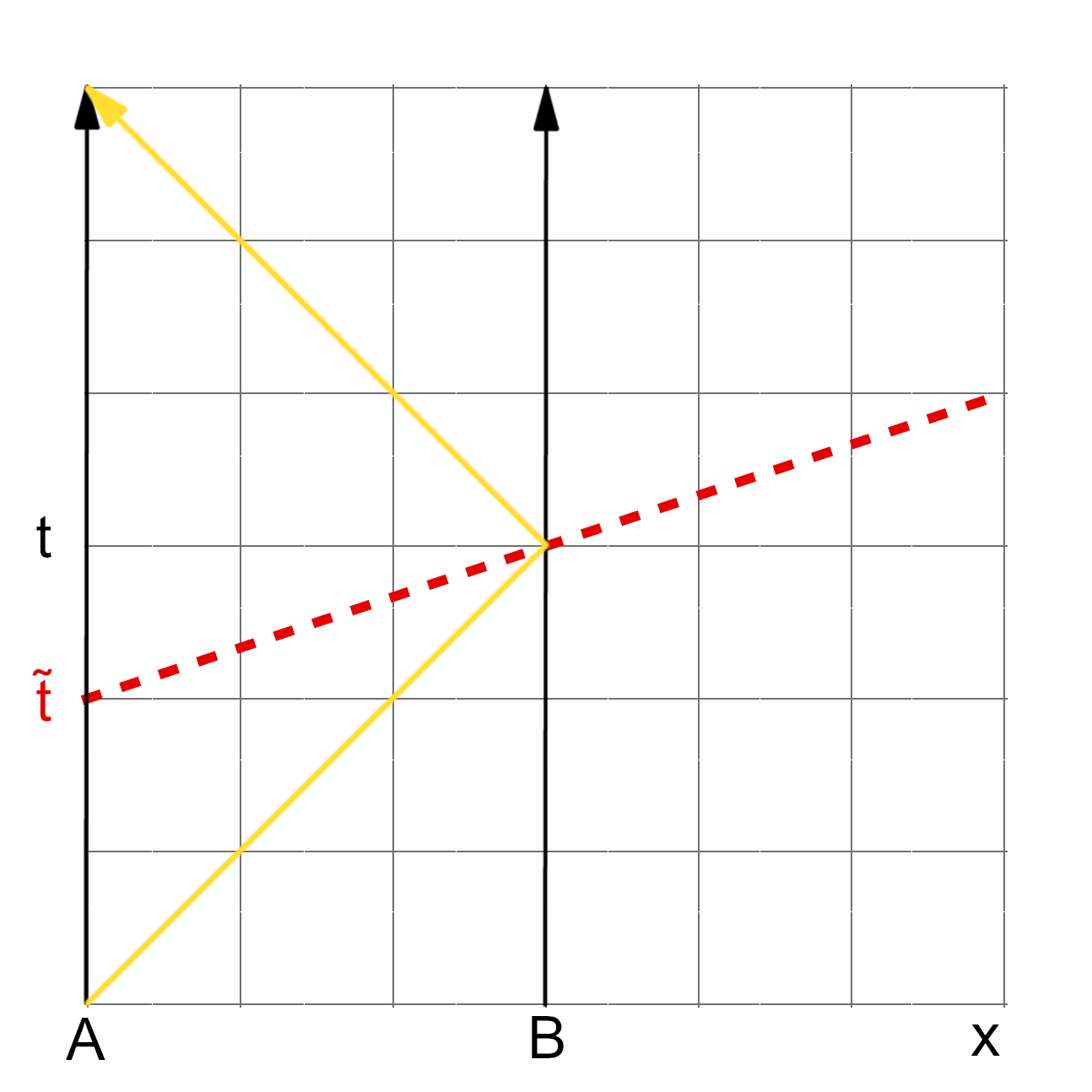
In his book “The Philosophy of Space and Time” (original German version 1928) the science philosopher Hans Reichenbach articulates the idea that distant simultaneity in relativity theory is just an arbitrary convention like all coordinate definitions.

The definition of simultaneity given by Einstein, see eq. (3.1.), defines the time of arrival of the light ray at B as the mid-point between the time that the light was sent from A and the time that it returned to A. According to Reichenbach this definition is not compelling; any time will do provided it comes after $t_{A}$ and before ${\bar{t}}_{A}$ :

7.2

{\tilde{t}}_{B} : = t_{A} + ε ({\bar{t}}_{A} - t_{A}), 0 < ε < 1

Under this alternative rule the forward and backward velocities of light between A and B are no longer equal; they are $c / 2 ε$ and $c / 2 (1 - ε)$ , respectively.
The round-trip velocity of light, measured with one clock, is still $c$ so that $c ({\bar{t}}_{A} - t_{A}) = 2 (x_{B} - x_{A})$ , which is Einstein's definition of distance. This is the only quantity that is directly observable.

The difference between Einstein time (3.1.) and Reichenbach time (7.2) then comes out as

7.3

t_{B} - {\tilde{t}}_{B} = \frac{1}{2} κ ({\bar{t}}_{A} - t_{A}) = κ (x_{B} - x_{A}), - 1 < κ < 1

with the shift constant $κ : = 1 - 2 ε$ .

Ruimtetijddiagram — Fig.7.1 Reichenbach synchronization: time $\tilde{t}$ lags behind Einstein time for positive shift coefficient $κ$ .

Reichenbach synchronization amounts to a shift in the setting of each inertial clock with respect to Einstein time by the amount $\tilde{t} - t = - κ x$ proportional to its displacement from the origin.
The description is empirically equivalent to Einstein’s because the round-trip velocity of light still has the established value.