Fundamentals of Time and Relativity

In a Lorentz velocity boost, the lines of simultaneity and same-position are altered. It is obvious from the Fig.5.2, that these lines are rotated towards each other over the same angle, and the spacing is also changed. To determine the scale factor, consider the triangle in Fig.5.2.

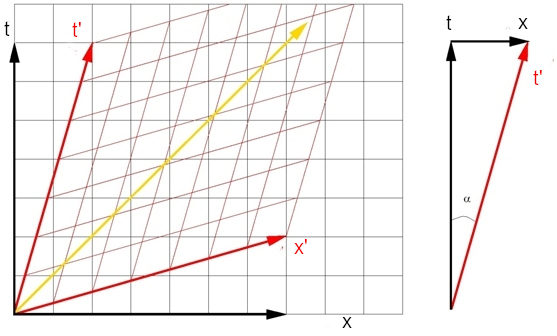
The tangent of the rotation angle $\tan \alpha =x(t)/t=v$ is the velocity of the moving frame (red) as seen from the stationary frame (black). Observer $O^{\prime }$ is at rest in the frame indicated by the red arrow, and reads the time between the origin and some event $(t^{\prime },0)$, simply as the proper time $\tau =t^{\prime }$ of  a co-moving clock.

However, observer $O$ sees this measurement as a combined measurement of a time interval $t$ and a distance $x$, and calculates the spacetime distance as ${\tau }^2=t^2-x^2$. Because this spacetime distance must be the same for both observers we have

The moving clock is slower than clocks in the stationary frame. This is the effect of time dilatation. The amount by which the clocks differ between two observers depends on the distance of the clock from the observer. A stationary observer at the origin sees a time difference $vx$ at distance $x$ from the origin.

The companion effect of Lorentz contraction

is similarly derived by considering the right-triangle composed of

1. a distance $x$ from the origin along the $x$-axis of the stationary system,
2. a 'time’ interval $vx$, and
3. the ‘proper’ distance $x^{\prime }$ from the origin to the event $(vx,x)$.