Synopsis Quantummechanica II

Rydberg-formule

Een belangrijk historisch feit in de ontwikkeling van de quantummechanica is dat de wiskundige exercitie op de vorige pagina, precies de gemeten golflengten $λ_{m n}$ voorspelt van het lijnenspectrum van waterstof beschreven door de Rydberg-formule ( Johannes Rydberg, 1888):

2.27

\frac{1}{λ_{m n}} = R_{H} (\frac{1}{m^{2}} - \frac{1}{n^{2}}) n > m

De evenredigheidsconstante wordt de rydbergconstante genoemd; deze heeft de experimenteel bepaalde waarde $R_{H} = {1,0974.10}^{7} m^{- 1}$ .

In het quantummechanische model van het waterstofatoom worden fotonen uitgezonden (of geabsorbeerd) als het elektron een “quantumsprong” maakt van een hoger naar een lager energieniveau (of van lager naar hoger bij absorptie). Omdat energie behouden is moet gelden dat de energie $ε_{m n}$ van het uitgezonden (of geabsorbeerde) foton gelijk is aan het energieverschil tussen de twee energieniveaus. Met de Einsteinrelatie (1.1) volgt

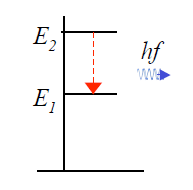
2.28

ε_{m n} = h \cdot f_{m n} = | E_{m} - E_{n} | m, n = 1,2,3,...

Na invullen van (2.22) voor de energie-eigenwaarden, blijkt dat de twee vergelijkingen (2.27) en (2.28) met elkaar in overeenstemming zijn als

2.29

R_{H} = \frac{R_{y}}{h c} = \frac{m e^{4}}{8 ε_{0}^{2} h^{3} c}

Hiermee is de experimentele rydbergconstante herleid tot een combinatie van fundamentele natuurconstanten, i.h.b. de lichtsnelheid $c$ en de constante van Planck $h$ . Dit spectaculaire resultaat van de quantummechanica werd in 1913 voor het eerst afgeleid door Niels Bohr.
Er blijken meer lijnen in het spectrum van het waterstofatoom voor te komen dan de Rydberg-formule kan verklaren. Dit komt o.a. door de ruimtelijke structuur van de atomen en de spin van het elektron.