Hoofdstuk 1. Opgaven

  • Je moet een wereldlijn kunnen tekenen van een lichtstraal in een ruimtetijddiagram.
  • Je moet van een object een wereldlijn kunnen tekenen in een ruimtetijddiagram.
  • Je moet van een gebeurtenis de coördinaten kunnen aflezen in een ruimtetijddiagram.
  • Je moet een betekenis kunnen toekennen aan punten en (wereld)lijnen in een ruimtetijddiagram.

§ 1.2

  1. Teken een ruimtetijddiagram met twee ruimtedimensies en één tijdsdimensie.
  2. Waarom kun je geen ruimtetijddiagram tekenen met drie ruimtedimensies en één tijdsdimensie?

§ 1.3

  1. Welke grootheid tekenen we in een ruimtetijddiagram langs de verticale as?
  2. Kan in een ruimtetijddiagram de lijn van boven naar beneden lopen? Zo nee, waarom niet?
  3. Teken het ruimtetijddiagram van een foton in vacuüm.
  4. Teken het diagram van een foton dat in vacuüm in de negatieve ruimterichting beweegt.

In water is de lichtsnelheid maar 0,75c.

  1. Teken het diagram van een foton dat door water beweegt.
  2. In het ruimtetijdpunt (w=1, x=4) gaat een lamp aan die gedurende 3 seconden aanblijft. De lamp zendt in vacuüm in alle richtingen licht uit. Teken het ruimtetijddiagram van deze gebeurtenissen.
  3. Als in het ruimtetijd diagram in ‘alle’ richtingen licht wordt uitgezonden, over hoeveel richtingen gaat het dan?
  4. Tussen welke tijdstippen wordt het punt x=6 belicht?

We rekenen vaak met de afgeronde waarde voor de lichtsnelheid van 3 ∙ 108 m/s. Is dan de afwijking van de correcte waarde meer of minder dan 1 %?

§ 1.4

Foucault

Gegeven is dat in figuur 1.7 voor hoek β 1,0º wordt gemeten. Van het draaiende spiegeltje is bekend dat het 440 omwentelingen per seconde maakt, terwijl de afstand MP 500 m bedraagt. Bereken hieruit de snelheid van het licht.

§ 1.5

A staat stil en B beweegt met constante snelheid v ten opzichte van A. A gooit op t = 0 een voorwerp met snelheid ½ v naar voren; ook B doet dit. Teken de wereldlijnen van A, B en van deze twee voorwerpen.

  1. Kunnen wereldlijnen elkaar snijden?
  2. Zo ja, wat is de betekenis van het snijpunt? Zo nee, waarom niet?
  3. Bekijk figuur 1.10. Geef de tijdstippen aan waarop de dame (de kronkelende wereldlijn) stilstaat.
wereldlijnen
Figuur 1.10 Wereldlijnen

Waarom is de wereldlijn in figuur 1.12 onmogelijk?

Afbeelding
Figuur 1.12 Onmogelijke wereldlijn

Wat is het verschil tussen een pad door de ruimte en een wereldlijn door de ruimtetijd?

§ 1.6

Stel: je zit op de achterbank van een auto. De auto staat in de file en je zit een beetje dromerig naar buiten te staren. Soms heb je dan wel eens even het gevoel dat de auto plotseling achteruit begint te rijden. Je schrikt wakker en kijkt nog eens goed. Dan blijkt het dat het de rij auto’s naast je is geweest die in beweging kwam.

  1. Leg uit, in termen van het eerste postulaat, waaraan je je vergissing bemerkt.
  2. Beschrijf een situatie uit het dagelijks leven waarbij je niet weet of je stilstaat of juist beweegt.

Meneer A zit in een remmende trein, mevrouw B staat stil op het perron. Beiden laten een tennisbal uit hun hand vallen.

  1. Komt de tennisbal van meneer A vlak voor zijn voeten op de grond, of beweegt die bij hem vandaan?
  2. Wordt dit door allebei waargenomen?
  3. En hoe zit dit voor de tennisbal van mevrouw B?

    4. Aan de antwoorden op bovenstaande vragen kun je zien dat beiden het erover eens zijn dat meneer A aan het versnellen is en mevrouw B niet.

  4. Als A en B nu eens niet ten opzichte van elkaar versnellen, kun je dan een experiment bedenken dat bewijst dat bijvoorbeeld A beweegt en B stil staat?
  1. Als je een inertiaalstelsel gekozen hebt (bijvoorbeeld in de hoek van een boot), waar houdt dit stelsel dan op?
  2. Kun je een bal een inertiaalstelsel uitgooien, net zoals je een bal uit een boot kunt gooien?

Het eerste postulaat zegt dat de natuurkundige wetten hetzelfde zijn in ieder inertiaalstelsel. Beantwoord nu de volgende vragen met een argumentatie:

  1. Gegeven dit postulaat, is er dan een fysisch onderscheid te maken tussen een inertiaalstelsel in rust en een inertiaalstelsel dat beweegt met constante snelheid?
  2. Gegeven dit postulaat, zou een object dezelfde kinetische energie moeten hebben in alle inertiaalstelsels?
  3. Gegeven dit postulaat, als je twee identieke experimenten zou uitvoeren in twee verschillende inertiaalstelsel, zou je dan exact dezelfde resultaten moeten krijgen?

Stel je twee boten voor. Boot 1 vaart met 2,5 m/s naar het oosten. De andere boot vaart met 5 m/s naar het oosten. We maken aan iedere boot een inertiaalstelsel vast met de x-as naar het oosten wijzend.

  1. Wat is de snelheid van boot 1, bezien vanuit het stelsel van boot 2?
  2. Wat is de snelheid van boot 2, bezien vanuit het stelsel van boot 1?

Einstein gebruikte twee postulaten (veronderstellingen) bij het opstellen van zijn speciale relativiteitstheorie. Noem de veronderstelling die Einstein zelf had bedacht en noem die welke door Galileï is bedacht.

Een lamp zendt in alle richtingen licht uit. We kijken alleen naar fotonen die naar links en rechts gaan.

Hoe snel gaan die ten opzichte van elkaar…

  1. volgens de Newton-theorie?
  2. volgens Einsteins postulaat?

In figuur 1.13 zijn twee gebeurtenissen A en B aangegeven. De hokjes hebben een hoogte en breedte van 1 lichtseconde. De oorsprong is het punt (0,0).

  1. Op welke tijdstippen vinden de gebeurtenissen A en B plaats?
  2. Hoever van de oorsprong vinden zij plaats?
Afbeelding
Figuur 1.13 Een w-x-diagram aflezen

In figuur 1.14 worden een rode en twee gele wereldlijnen gegeven die elkaar snijden in de oorsprong 0 (x=0, w=0).

  1. Wat stellen deze wereldlijnen voor?

    2. We stellen ons voor dat er een ontmoeting plaatsvindt tussen de zwarte waarnemer en ene Tachy-John (T-J) die met een snelheid van v=2c langskomt. De ontmoeting vindt plaats in de oorsprong. Zijn assenstelsel is in figuur 1.14 al rood weergegeven.

    Om zijn komst aan te kondigen stuurt T-J met regelmatige tussenpozen een lichtsignaal naar de zwarte waarnemer. De ruimtetijdpunten van waaruit de signalen vertrekken zijn met de letters A t/m I aangegeven. Hij blijft signalen zenden na de ontmoeting. Wij proberen dit probleem te analyseren aan de hand van fig. 1.15; hierin zijn lichtsignalen getekend die ontstaan in de punten A t/m I en die de vertrouwde loop hebben die we al eerder tegenkwamen.

  2. Hoe ervaart de zwarte waarnemer de hele ontmoeting (beschrijf de ontmoeting als een reeks van waarnemingen van de zwarte waarnemer)?
  3. Wat kun je zeggen over de frequenties (zo mogelijk kwantitatief) van de reeks signalen die de zwarte waarnemer ontvangt.

    4. Ook de zwarte waarnemer heeft de hele tijd een knipperlicht aanstaan.

  4. Teken met behulp van de tekentool de wereldlijnen van de signalen van dit knipperlicht. Beschrijf de hele ontmoeting nu vanuit het gezichtspunt van T-J.
  5. Hoe verhouden zich de frequenties van de signalen die T-J ontvangt, voor en na de ontmoeting?
  6. Leg met behulp van je antwoorden op vraag b en d uit dat hier sprake is van een schending van het eerste postulaat van Einstein.

Opm. Deze schending kan voorkomen worden; verderop besteden we daar aandacht aan.

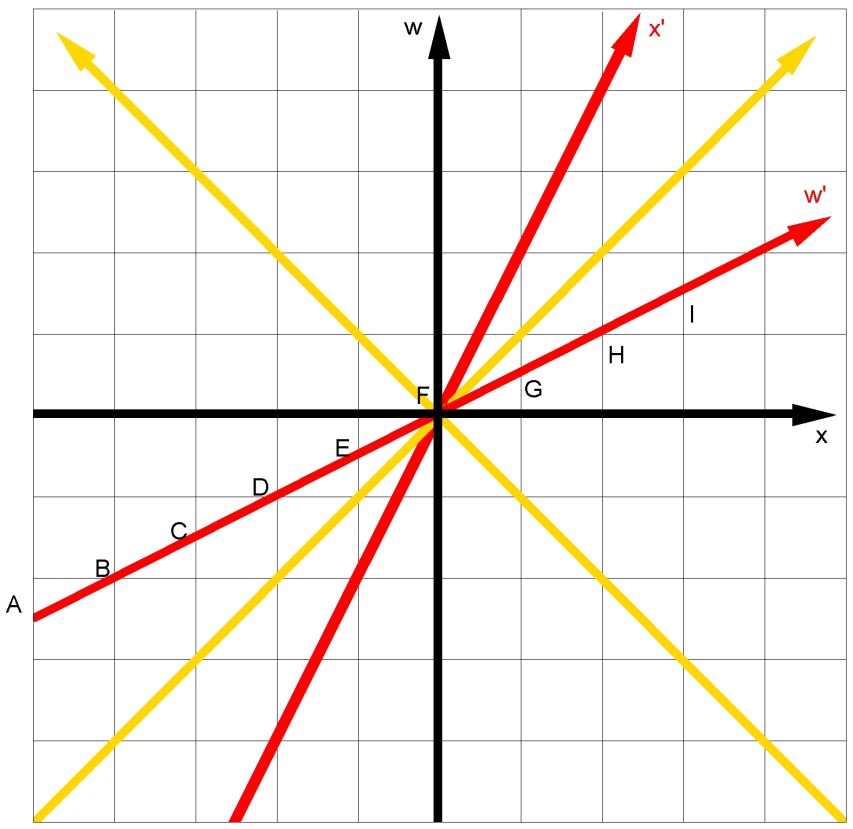Afbeelding
Figuur 1.14 Ontmoeting