We komen uit op een beeld, waarbij de rasters van inertiaalstelsels die bewegen
ten opzichte van het zwarte stelsel platgedrukt zijn zoals het rode stelsel in
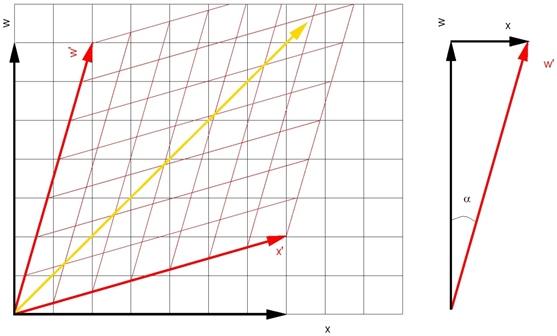
figuur 2.7a. De zwarte vierkantjes worden samengedrukt tot ruitvormige vierhoeken,
maar merk op dat de richting van wereldlijnen van lichtdeeltjes, die evenwijdig
lopen aan de diagonalen van de ruit, bij deze vervorming onveranderd blijft.
In figuur 2.7a is de getrokken rode lijn de wereldlijn van Arnold. In het zwarte
stelsel heeft Arnold snelheid, in zijn eigen stelsel niet. Arnold zegt dus dat de
rode lijn voortdurend zijn plaats x' = 0 weergeeft. De lijn x=0 in
het zwarte stelsel is niets anders dan de tijd-as (w-as) in dat zwarte stelsel. Op
dezelfde wijze is de rode lijn de tijd-as w' in het stelsel van Arnold.
Hier ligt een fundamenteel onderscheid tussen de theorie van Einstein en de
Newtonse natuurkunde. Bij Newton zijn plaats en snelheid relatief (hangen van de
waarnemer af). De tijd is absoluut, en is dus gelijk voor alle waarnemers.
Bij Einstein zijn plaats en snelheid ook relatief. Eén snelheid echter is
dat niet: de lichtsnelheid. Dit absoluut zijn van de lichtsnelheid leidt tot een
draaiing van de lijnen die gelijke tijdstippen met elkaar verbinden: de tijd (of
gelijktijdigheid) moet relatief worden. Hoeveel die lijnen ten opzichte van de
zwarte assen draaien, hangt af van de snelheid ten opzichte van het zwarte stelsel
waarmee de waarnemers door de ruimte bewegen.
Je ziet ook dat de nieuwe ruimte- en tijdas allebei dezelfde hoek maken met de
oude assen, en met de wereldlijn van een lichtsignaal. Daarom zal een punt op die
wereldlijn weer worden beschreven door gelijke componenten langs de x'- en w'- as,
hoewel we ons nog even niet druk maken over de getalswaarden die we bij de
schaalverdeling langs die assen moeten zetten. Deze afbeelding laat zien dat het
tweede postulaat van Einstein maakt dat ruimte en tijd niet meer op een objectieve
wijze van elkaar te scheiden zijn, en dat hun onderlinge relatie afhangt van de
snelheid waarmee we bewegen. Daarom hanteren we graag één begrip dat
hetzelfde is voor alle waarnemers: niet ruimte, niet tijd, maar ruimtetijd.
Het schenkt een zekere voldoening om op grond van zuiver kwalitatieve argumenten
tot zulke verrassende inzichten te komen. Toch is dit een goed moment om iets
kwantitatiefs te zeggen over de hellingshoeken van het rode raster. Als de rode
reizigers de snelheid v hebben, verplaatsen ze zich in een tijdsduur t
over een afstand
. Met
de afspraak dat
geeft
dat:
Dat kunnen we ook schrijven als
Bekijk nu de driehoek met de zijden w, w' en x in het ruimtetijddiagram figuur
2.7b. In deze driehoek zien we dat voor de tangens van de hoek
(de hoek tussen de w-as en de w'-as)
geldt:
Hieruit volgt dat:
De relatieve snelheidsparameter v/c wordt gewoonlijk weergegeven als
bèta:
en die notatie zullen we vaak aanhouden. Omdat de verhouding
tussen twee snelheden weergeeft, is het een puur getal
onafhankelijk van de keuze van natuurkundige eenheden. Merk op dat ook de tangens
van de hoek tussen de x-as en de x'-as gelijk is aan
.