Hoofdstuk 3. Opgaven

  • Je moet in een ruimtetijddiagram snelheden kunnen aflezen in verschillende stelsels.
  • Je moet snelheden kunnen optellen volgens de formule van Einstein.
  • Je moet kunnen aangeven welke gebeurtenissen invloed op elkaar kunnen uitoefenen en uitleggen waarom dat zo is.

§ 3.1

Het lijkt er op dat in figuur 3.1 causaliteit gered kan worden door het punt 2 twee tijdseenheden omhoog te schuiven: nu komt ook in het rode stelsel gebeurtenis 2 na gebeurtenis 1. Zo lijkt alles in orde, zowel in het zwarte als in het gekleurde stelsel.

De hokjes zijn weer zo ingedeeld dat zowel horizontaal als verticaal de lengte van een hokje met 1 lichtseconde overeenkomt. Stel dat in figuur 3.8 in het ruimtetijdpunt 1 het schot wordt gelost, en dat in punt 2 tante Sidonia neervalt.

  1. Bepaal in het zwarte stelsel de snelheid van de kogel, als die van punt 1 naar punt 2 gaat.
Afbeelding
Figuur 3.8 De snelheid van de kogel

§ 3.2

Afbeelding
Figuur 3.2 Is de lichtsnelheid een constante?

In figuur 3.2 wordt iets weergegeven dat in tegenspraak is met het tweede postulaat van Einstein.

  1. Hoe luidt dat tweede postulaat?
  2. Geef aan wat er in de figuur daarmee in strijd is.

§ 3.3

Afbeelding
Figuur 3.9

In bovenstaande figuur 3.9, een kopie van de figuur 3.3, heeft een aantal ruimtetijdpunten een naam (A t/m G) gekregen. Hieronder volgt een aantal vragen, in de trant van: "wat is de betekenis van de lengte van het lijnstuk CD in het zwarte stelsel?", met als bedoeld antwoord: "het is de verplaatsing van de trein in het zwarte stelsel, gedurende 4 zwarte tijdseenheden."

  1. Wat is de betekenis van de lengte van CE in het zwarte stelsel?
  2. Wat is de betekenis van de lengte van DE in het zwarte stelsel?
  3. Wat is de betekenis van de lengte van AD in het rode stelsel?
  4. Wat is de betekenis van de verhouding CD/AC?
  5. Noem een lijnstuk in het rode stelsel dat dezelfde betekenis als CE in het zwarte stelsel heeft.
  6. Is er een lijnstuk, en zo ja welk, aan te wijzen dat in het rode stelsel dezelfde betekenis heeft als CD in het zwarte stelsel?
  7. Welk lijnstuk in het zwarte stelsel heeft dezelfde betekenis als AG in het rode stelsel?

    8. De blauwe lijn, die de beweging van de hardloopster in het zwarte stelsel aangeeft, verdeelt lijnstuk DG in twee gelijke delen DF en FG.

  8. Wat is de betekenis van de lengte DG in het rode stelsel?
  9. Waarom geldt: DF = FG?

    10. De hardloopster besluit van looprichting om te draaien (nieuwe snelheid -1/2 c t.o.v. de trein). In het ruimte-tijdpunt F keert zij van bewegingsrichting om.

  10. Teken haar wereldlijn. Wat merk je op?

De bedoeling is dat je een figuur als figuur 3.3 met de tekentool zelfstandig tekent, aan de hand van de volgende aanwijzingen.

  1. Teken zwarte assen.
  2. Een trein heeft snelheid 0,8 c ten opzichte van het zwarte frame. Teken de wereldlijn van de trein. Maak het coördinatenstelsel van de trein af met een x'-as.
  3. In de trein rent een jongen met snelheid 0,5 c, gemeten in het stelsel van de trein, naar voren.
  4. Kies een willekeurig punt op de wereldlijn van de trein. Geef met een lijn alle punten, die in het stelsel van de trein dezelfde plaatscoördinaat hebben, als dit punt aan.
  5. Pas op het oog 0,5 maal de afstand die het licht in het treinstelsel heeft afgelegd af op de net getekende lijn. Teken de wereldlijn van de hardloper.
  6. Meet zijn snelheid in het zwarte stelsel.

§ 3.4

Beantwoord de volgende vragen over de formule:

u= u'+v 1+ u' ⋅ v c 2
  1. Leg uit dat voor snelheden veel kleiner dan c bovenstaande formule overgaat in u = u' + v.
  2. Ten opzichte waarvan worden u, v en u' gemeten?

    3. Zie figuur 3.3. Daarin beweegt een trein met snelheid ½ c ten opzichte van het zwarte stelsel. In de trein rent een meisje met snelheid ½ c, gemeten ten opzichte van de trein, naar voren.

  3. Bereken haar snelheid ten opzichte van het zwarte stelsel.
  4. Controleer of aflezing van deze snelheid uit figuur 3.3 hetzelfde resultaat oplevert.
Afbeelding
Figuur 3.3 Optelling van snelheden volgens Einstein

In het atoommodel van Bohr cirkelt het elektron in de binnenste schil met snelheid Z ⋅ c / 137 rond de kern. Hierin is Z het atoomnummer van de kern Is het redelijk om deze beweging met behulp van de Newtonse mechanica te beschrijven voor:

  1. Een waterstofatoom?
  2. Een goudatoom?
  3. Is de wereldlijn van de hardloopster die je in opgave 37, onderdeel j, hebt getekend, in overeenstemming met boven gegeven formule?
  4. u' en v komen symmetrisch in de formule voor, d.w.z. je kunt u' door v vervangen en v door u' zonder dat de formule verandert. Breng met behulp van een getallenvoorbeeld (geen berekening nodig!) onder woorden wat dit betekent.
  5. * Een straaljager vliegt met een snelheid van 500 m/s. De straaljager vuurt een raket af met een snelheid van 3000 m/s. Bereken hoe snel wij de raket zien vliegen op aarde.

Volgens Einstein moeten snelheden opgeteld worden volgens de formule in de vorige opgave. De regel van Newton is eenvoudiger: u = u' + v.

  1. Als je v = c neemt, welke snelheid krijg je dan voor u?
  2. In welke gevallen komen de uitkomsten van de twee formules exact overeen?

Een sterrenstelsel beweegt met snelheid 2/3 c bij ons vandaan. Het licht heeft snelheid c ten opzichte van dit sterrenstelsel.

  1. Hoe groot is de snelheid van het licht ten opzichte van ons?

    2. Een sterrenstelsel beweegt zich met snelheid 2/3 c bij ons vandaan. Een ander stelsel beweegt even snel bij ons vandaan, in tegenovergestelde richting.

  2. Kan het licht van het ene stelsel het andere ooit bereiken?
  3. Bereken met behulp van de formule de onderlinge snelheid van de stelsels.
Afbeelding
Figuur 3.10

Drie bankrovers zijn met hun buit op de vlucht voor de politie. Hun vluchtauto gaat met een snelheid van ¾ c. De politieauto gaat maar met een snelheid van ½ c. Deze beide snelheden worden gemeten ten opzichte van de grond. Een agent vuurt een kogel af met een snelheid van 1/3 c. Deze laatste snelheid is gemeten ten opzichte van de politieauto.

  1. Bereikt de kogel de boeven volgens Newton?
  2. Bereikt de kogel de boeven volgens Einstein?
  3. Waarschijnlijk heb je onderdeel beantwoord vanuit een waarnemer die zich op de grond bevindt. Beantwoord onderdeel b nu, vanuit het gezichtspunt van de politie, de boeven en de kogel. Vul de gaten in onderstaande tabel.

Snelheid van →

t.o.v. ↓

Grond

Politie

Boeven

Kogel

Ontsnappen ze?

Grond

0

1/2 c

3/4 c



Politie


1/3 c


Boeven




Kogel




§ 3.5

Karel heeft een hele sterke zaklamp en hij wil daarmee laten zien dat het mogelijk is om sneller dan het licht informatie te sturen. Hij vraagt Jan en Piet om 1 km uit elkaar te gaan staan. Karel monteert zijn zaklamp op een platenspeler die een maal per seconde ronddraait en zet deze platenspeler op 100.000 km afstand van Jan en Piet (zie figuur 3.11).

Afbeelding
Figuur 3.11 Situatie met Jan, Piet en de zaklamp
  1. Jan ziet de zaklamp voorbij flitsen. Hoe lang duurt het voordat Piet de lichtstraal ook ziet?
  2. Jan pakt een laserpistool en schiet op Piet. Hoe lang duurt het voordat Piet geraakt wordt? Kun je concluderen dat de bundel van de zaklamp sneller dan het licht gaat? Je kunt zeggen dat bovenstaand voorbeeld niet eerlijk is. Immers, de fotonen uit de zaklamp gaan zelf niet sneller dan het licht.
  3. Karel zegt nu dat Jan pas mag schieten als hij het licht van de zaklamp voorbij ziet komen. Tegen Piet zegt Karel dat hij moet bukken als hij de zaklamp ziet. Is Piet op tijd om het laserpistool te ontwijken?
  4. Karel zegt dat er nu informatie sneller dan het licht is verstuurd. Ben je het met hem eens?
  5. Waarom (niet)?

Het is 1900. In Hamburg (Noord-Duitsland) is om 12 uur 's nachts een misdrijf gepleegd. Een zekere Albert E., geboren te in Ulm (Zuid-Duitsland) wordt verdacht. Hij beweert echter zijn onschuld te kunnen bewijzen! Dat gaat als volgt:

  • Hij kan aantonen dat hij om 19 uur (5 uur voor het misdrijf) nog in München was. De afstand München-Hamburg is 600 km.
  • Het snelste vervoermiddel (in 1900) haalt 100 km/h.

De politie ziet niet in dat dit een bewijs is, dus voegt Albert E. er nog aan toe:

  • De minimale reistijd tussen Hamburg en München bedraagt 6 uur.
  • Omdat hij om 19 uur nog in München was, kan hij niet om 24 uur in Hamburg geweest zijn.

Toen zij dit begrepen hadden, raadde E. de politie aan op vergelijkbare manier andere mogelijke daders uit te sluiten. Op een kaart (figuur 12) rond Hamburg worden hiertoe cirkels getrokken, met straal 100, 200, 300, enz. km. Bij die cirkels worden relevante tijdstippen gezet.

  1. Vraag: welke betekenis hebben deze tijdstippen voor dit misdrijf?
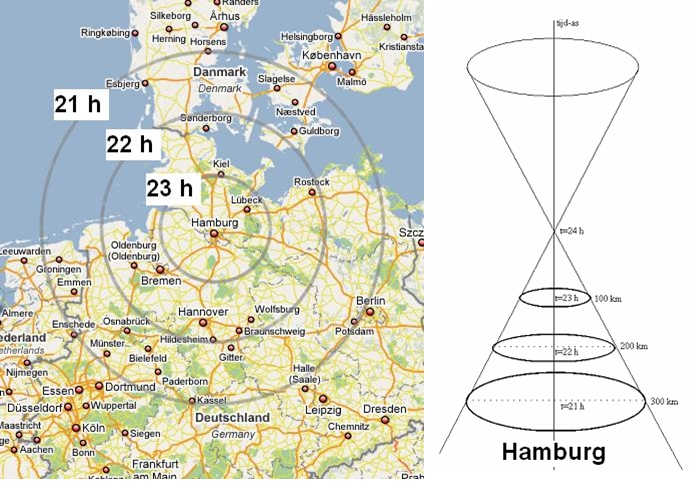Afbeelding
Figuur 3.12 Onschuldigen uitsluiten
Figuur 3.13 De schuldige bevindt zich binnen de kegel

Vervolgens bedenkt men dat deze informatie mooier is weer te geven in de (2dimensionale) weergave van een andere 3-dimensionale figuur 3.13. Die is hiernaast getekend.

Alle mogelijke verdachten die kunnen aantonen dat zij op enig moment een plaats- en tijdcoördinaat hadden die buiten de getekende kegel vallen, zijn onschuldig!

Dit idee kun je ook op slechts 1 ruimtedimensie toepassen. De cirkels rond Hamburg zouden vervangen moeten worden door lijnstukken met als lengte de diameter van de cirkel die zij vervangen.

De kegel verandert dan in een eenvoudiger figuur, met slechts twee dimensies: één voor de tijd en de andere voor de plaats.

Merk op dat de onschuld van Albert E. niet bewezen had kunnen worden als hij de beschikking had gehad over een voertuig dat 200 km/h kon halen!

Figuur 3.13 zou dan vervangen moeten worden door een kegel met een grotere tophoek. En binnen die grotere kegel zou het punt met coördinaten (München, 19 h) wèl vallen!

In figuur 3.14 zijn twee gebeurtenissen A en B getekend, die voor een zwarte waarnemer niet gelijktijdig zijn.

  1. Teken een stelsel waarin de gebeurtenissen A en B wel gelijktijdig plaatsvinden.
  2. Bepaal de snelheid van dit stelsel.
  3. Leg nu uit dat tussen de gebeurtenissen B en A geen causaal verband kan bestaan.
Afbeelding
Figuur 3.14 Causaal verband?
Afbeelding
Figuur 3.15 Lichtkegels en causaal verband
  1. Teken in fig. 3.15 de lichtkegels van de gebeurtenis P : (x,w)= (5,3)
  2. Teken een stelsel waarbij Q: (7,4) voor P plaatsvindt. Voor welke snelheden is dit het geval?
  3. Laat zien dat de Q niet voor P plaats kan vinden als we kiezen Q: (4,5).
  4. Met welke snelheid zou een signaal verstuurd moeten worden vanuit P om in Q aan te komen?
  5. We hebben twee gebeurtenissen P:(x1,w1) en Q: (x2,w2). Geef de algemene conditie dat deze twee gebeurtenissen oorzakelijk samenhangen.

We stellen ons voor dat er een ontmoeting plaatsvindt tussen de zwarte waarnemer en ene Tachy-John (T-J) die met een snelheid van v=2c langskomt. De ontmoeting vindt plaats in de oorsprong. In hoofdstuk 1 analyseerden we dit probleem aan de hand van het ruimtetijddiagram uit figuur 3.16:

Afbeelding
Figuur 3.16 Ontmoeting

We zagen dat er problemen ontstonden door een schending van het 1e postulaat van Einstein: zwart neemt de beweging van T-J anders waar dan T-J die van zwart waarneemt.

Een nadere beschouwing doet ons inzien waar deze schending vandaan komt. T-J zendt in de figuur alleen signalen uit in zijn positieve ruimterichting! En deze signalen na het passeerpunt lopen ook nog in de negatieve tijdrichting van T-J.

  1. Leg dit uit.
  2. Teken nu een herziene versie van figuur 3.16 waarin op de twee genoemde punten correcties zijn aangebracht.
  3. Hoe ervaart de zwarte waarnemer de hele ontmoeting (beschrijf de ontmoeting als een reeks van waarnemingen van de zwarte waarnemer)?
  4. Is op deze wijze wel voldaan aan Einsteins 1e postulaat? Ga daartoe na hoe T-J de ontmoeting zou ervaren, waarbij de zwarte waarnemer met regelmatige tussenpozen lichtsignalen uitzendt.

    5. Zoals je zal zijn opgevallen, moet er een prijs betaald worden om aan Einsteins eisen te voldoen: sommige signalen die T-J in zijn positieve tijdrichting uitzendt, lopen in de negatieve zwarte tijdrichting.

  5. Is iets vergelijkbaars aan de hand met de signalen die de zwarte waarnemer uitzendt?
  6. T-J's lichtkegel is gedraaid t.o.v. die van de zwarte waarnemer. Treedt zo een draaiing ook wel eens op bij waarnemers die ten opzichte van elkaar een lagere snelheid dan c bezitten?
  7. Breng onder woorden welke problemen met causaliteit zouden ontstaan als er mensen (of machines, of signalen) sneller dan het licht zouden kunnen gaan.