4.2 Tijdrek

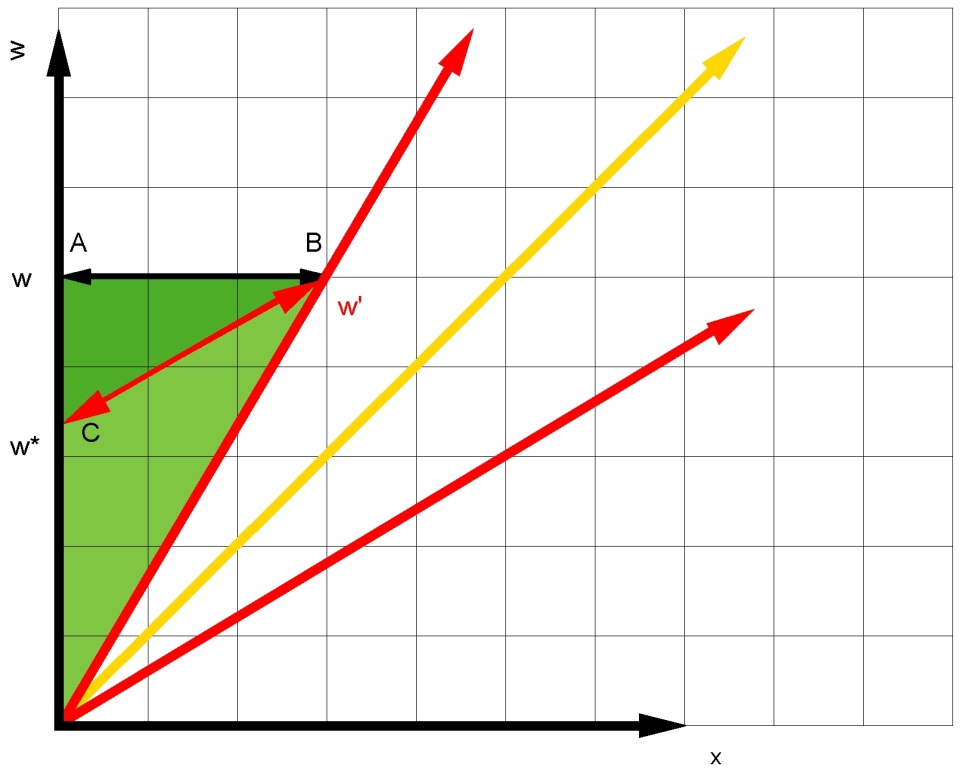
Als rechtgeaard relativist vraag je je nu natuurlijk af hoeveel langzamer een bewegende klok dan wel loopt. Om dat te bepalen gebruiken we weer een stukje meetkunde van het platte vlak.

In figuur 4.2 zie je twee groene rechthoekige driehoeken: een grote, ABO, en deels daaroverheen een kleine in donkerder groen, ABC.

We hebben weer te maken met gelijkvormige driehoeken, zodat er een vaste verhouding bestaat tussen corresponderende zijden. Daarom geldt dat AB/AO = AC/AB.

Merk op dat AB/AO = v/c = β en AO = w, zodat AB = wv/c = β w. Ook kunnen we uit figuur 4.2 meteen aflezen dat AC = w - w*. Als we deze uitdrukkingen invullen in de verhoudingsformule, vinden we β = (w - w*)/β w.

Om die vergelijking op te lossen voor w, hoeven we alleen maar beide kanten te vermenigvuldigen met β w, alle termen met w naar één kant te brengen en w buiten haakjes te halen. We verkrijgen dan de formule w = w*/(1 - β²)

Uit de relatie w =γ²w* volgt dat de evenredigheidsconstante γ die we zoeken, gegeven wordt door de wortel uit 1/(1 - β²). We noemen γ de relativistische snelheidsfactor.
Voor de verhouding tussen de kloksnelheden vinden we:

w^{'} = w \cdot \sqrt{1 - β^{2}}

Einsteins formule voor tijdrek

Het verband tussen de tijdsaanduiding tussen twee klokken die ten opzichte van elkaar bewegen met snelheid v wordt gegeven door:

t' = t \cdot \sqrt{1 - β^{2}} = \frac{t}{γ} γ = \frac{1}{\sqrt{1 - β^{2}}}

Legenda: t is een tijdstip op een stilstaande klok, t' is een tijdstip op een bewegende klok met snelheid v; hierin is $β = v / c$ de relatieve snelheidsparameter.

Laten we even stilstaan bij een paar interessante aspecten van deze fraaie formule. Zoals eerder gezegd zien we dat w'= c · t' inderdaad altijd kleiner zal zijn dan w = c · t, omdat de waarde onder het wortelteken altijd tussen 0 en 1 ligt (want v is natuurlijk altijd kleiner dan c). Uiteraard geldt daarbij dat w' = w als v = 0. Iets griezeliger is het feit dat w' naar 0 gaat als v dichter bij c komt, wat inhoudt dat de tijd 'stilstaat' op een klok die zich voortbeweegt met de lichtsnelheid. In dat unieke stelsel gaat het begrip tijd niet meer op: de 'samengedrukte' kaders die we zo ijverig hebben getekend voor bewegende waarnemers worden gereduceerd tot een enkele lijn, waarop geen onderscheid meer te maken valt tussen ruimte en tijd.

We hebben gezien dat de ruimtetijddiagrammen een gebruikersvriendelijk hulpmiddel vormen om vat te krijgen op de relativiteitstheorie. Toch kun je de gelijkwaardigheid van verschillende inertiaalstelsels nooit rechtstreeks zichtbaar maken in één enkele afbeelding. Maar diezelfde asymmetrie tussen stelsels doet zich ook voor bij een weergave in formules, waar je ook altijd maar één formule tegelijk hanteert, bijvoorbeeld die voor de tijdsuitrekking.

We hebben bij onze berekeningen gebruikgemaakt van de vertrouwde euclidische meetkunde in het platte vlak. Maar mogen we het euclidische begrip van gelijkvormigheid wel zomaar toepassen in een context waarin we verschillende ruimtetijdstelsels met elkaar vergelijken? Zijn de voorschriften van Euclides' wet geldig in het vlak van de ruimtetijd?

Nou nee, eigenlijk niet. Het probleem is niet zozeer dat het rode kader samengedrukt is, als wel dat de eenheden langs de rode assen herschaald zijn. Omdat de overeenkomstige zijden van de verschillende driehoeken echter altijd bij hetzelfde stelsel horen, valt de schaalfactor weg uit de verhoudingen tussen zulke zijden. De verhouding tussen rode lijnstukken mogen we dus vergelijken met die tussen zwarte lijnstukken, ondanks het verschil in schaal met een relativistische snelheidsfactor γ.

Een astronaute zit in een raket met snelheid 0,5 c t.o.v. de aarde. Ze verliest 120 s het radiocontact. Hoelang denkt de controletoren op aarde dat er geen contact was?

T.22

w´= w/γ . Omdat w´=c.t´ en w=c.t geldt dan ook t´= t/γ. t´= 120 s.

\begin{array}{l} γ = 1 / \sqrt{1 - {(0,5)}^{2}} = 4 / 3 \\ t = 4 / 3 \cdot 120 = 160 s . \end{array}

Het contact is op de controletoren 160 s verbroken.