5.1 Lorentz-transformaties

Tot nu toe hebben we het steeds gehad over verschillende referentiekaders met elk hun eigen coördinatenstelsel, zoals het zwarte en het rode stelsel. Deze beschouwingen werpen een belangrijke algemene vraag op over de relatie tussen coördinatenstelsels die horen bij twee inertiaalwaarnemers.

Als een gebeurtenis P de coördinaten (w, x) heeft in het zwarte (rust)stelsel en de coördinaten (w’, x’) in een rood stelsel dat zich voortbeweegt met een relatieve snelheid β = v/c, wat is dan het algemene verband tussen de coördinaten (w, x) en (w’, x’)? Kortom, we willen weten wat de uitdrukking van de coördinaten w’ en x’ is in termen van w en x (of andersom). Als we dan het ‘wanneer en waar’ van een gebeurtenis weten in het ene stelsel, kunnen we direct berekenen wanneer en waar die plaatsvond in het andere. Dus als de rode waarnemer meldt dat hij op een bepaald tijdstip en op een bepaalde plaats iets laat ontploffen, dan kan de zwarte waarnemer weten waar en wanneer deze explosie voor hem plaats vindt! Je snapt natuurlijk dat deze relatie afhangt van β. We zullen het verband afleiden met behulp van dezelfde soort figuren en meetkundige verbanden die we tot nu toe hebben gebruikt.

De gezochte relaties zijn de befaamde Lorentz-transformaties, die ons in staat stellen gegevens van het ene stelsel naar het andere te vertalen of transformeren. We kennen er al een voorbeeld van: de formule voor de tijdsuitrekking, want die geeft een eenvoudige uitdrukking voor w’ in termen van w. Hieronder een meetkundige afleiding van de relatie tussen twee coördinatenstelsels.

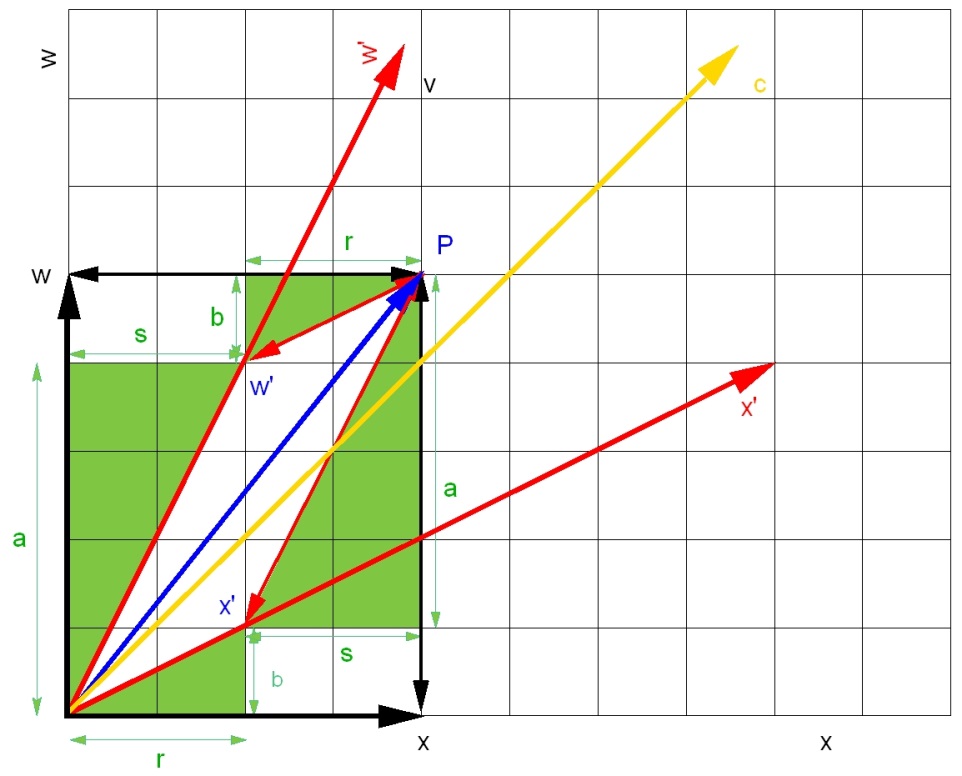
De verbanden die we zoeken zijn eenvoudig af te leiden uit de figuur 5.1, dankzij het feit dat de groene driehoeken gelijkvormig zijn of zelfs alleen gedraaid.

De gebeurtenis P aangegeven in blauw, heeft op de assen van het rode coördinatenstelsel de coördinaten w’ en x’. In het zwarte ruststelsel zijn de coördinaten ervan w en x.

Uit de figuur is af te lezen dat $w = a + b$ en $x = r + s$ .

In paragraaf 3.4 hebben we al uitgebreid gebruik gemaakt van het feit dat:

\frac{s}{a} = \frac{v \cdot t}{c \cdot t} = \frac{b}{r} = β

In de uitleg over de tijdsuitrekking hebben we besproken dat $a = γ \cdot w'$ , waarbij

γ = \frac{1}{\sqrt{1 - β^{2}}}

Invullen in de verhouding $s / a = β$ levert op dat $s = β \cdot γ \cdot w'$ . Uit de gelijkvormigheid van de grote en kleine driehoeken concluderen we dat ook moet gelden dat $r = γ \cdot x'$ en $b = β \cdot r = β \cdot γ \cdot x'$ .

Nu hoeven we alleen maar de uitdrukkingen uit stap 3 in te vullen in de formules uit stap 2. We vinden dat

w = a + b = γ \cdot w' + β \cdot γ \cdot x'

en

x = r + s = γ \cdot x' + β \cdot γ \cdot w'

Deze eenvoudige transformatieregels om van de ruimtetijdcoördinaten (w’, x’) over te gaan naar de coördinaten (w, x) hebben alle symmetrie-eigenschappen die we op grond van de figuur zouden verwachten. Bovendien gedragen ze zich op de juiste manier in het limietgeval $v \to 0$ (waarbij $β \to 0$ en $γ \to 1$ ).

Zo vinden we de formules voor de Lorentz-transformaties.