We beginnen met de impuls van een bewegend deeltje en bekijken de verschillen
tussen de klassiek newtoniaanse theorie en de speciale relativiteitstheorie.
In de mechanica van Newton wordt de bewegingstoestand van een deeltje bepaald
door ten eerste zijn massa m en ten tweede zijn snelheid
of impuls
, die ook wel
'hoeveelheid beweging' wordt genoemd (zie appendix 7.3). Snelheid en impuls zijn,
net als kracht en versnelling, vectoren: ze hebben een richting en een
grootte. In een wereld met drie ruimtelijke dimensies is zo'n vector een pijl met
componenten langs de x-, y-, en z-as. In onze miniwereld, die slechts
één ruimtelijke dimensie heeft, kunnen deze vectoren alleen langs de
positieve of negatieve x-as gericht zijn: px= m · v of px=
- m · v.
Je zult er inmiddels van doordrongen zijn dat ruimte en tijd in de
relativiteitstheorie nauw met elkaar verweven zijn. Om recht te doen aan het
begrip 'ruimtetijd' moeten we een natuurlijke tijdcomponent, die we zullen noteren
als p0, voor de impulsvector definiëren, zodat we een
ruimtetijdvector (p0,px) krijgen analoog aan de
positievector (w,x). Er is hiervoor een zeer natuurlijke keuze te doen.
Als het deeltje een pad door de ruimte aflegt is de impulsvector op een gegeven
moment altijd gericht langs de raaklijn aan het pad door de ruimte in het punt
waar dat deeltje op dat moment is. In de ruimtetijd beweegt het deeltje zoals we
weten langs een wereldlijn en je verwacht dat de ruimtetijd impulsvector gericht
is langs de raaklijn aan de wereldlijn. Omdat het pad in de ruimte niets anders is
dan de projectie van de wereldlijn op de ruimte, moet het zo zijn dat de projectie
van de ruimtetijd impulsvector de ruimtelijke impulsvector geeft. De tijdcomponent
van de ruimtetijd impulsvector kan daaruit eigenlijk al bepaald worden zoals uit
een eenvoudig voorbeeld moge blijken.
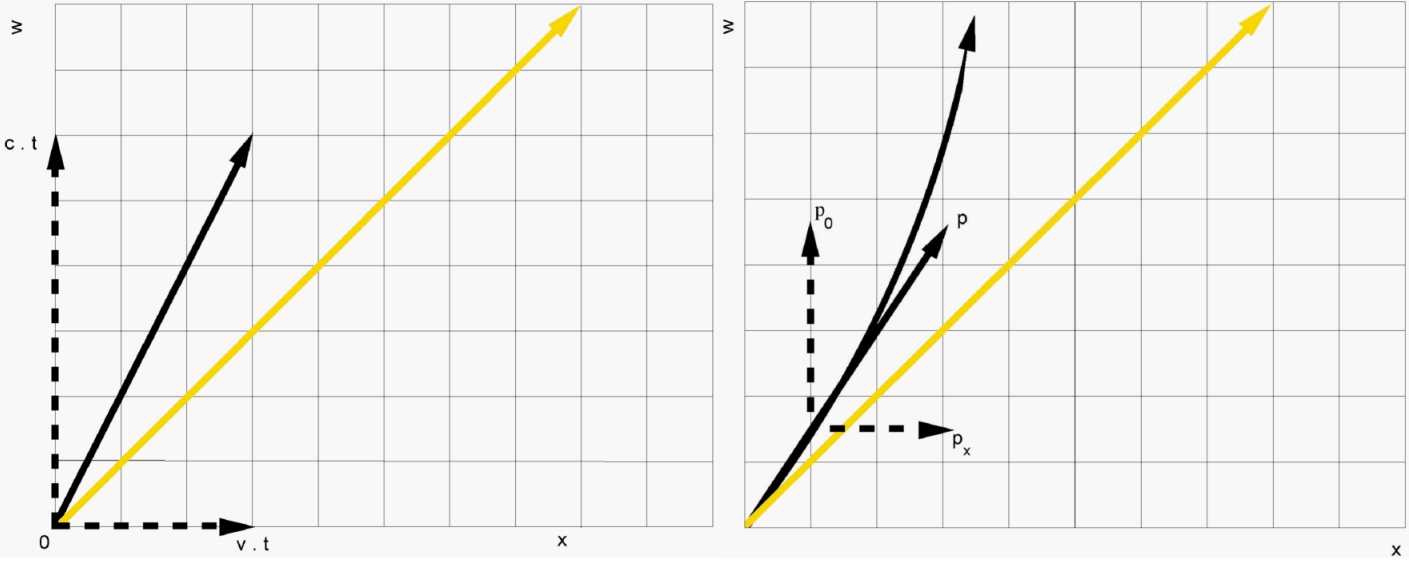
We beschouwen als voorheen het geval van een deeltje dat met een constante
snelheid v in de positieve x-richting beweegt. De wereldlijn van het
deeltje is de bekende lijn die een hoek α met de tijdas maakt en de
projectie daarvan is inderdaad gewoon het pad waarlangs het deeltje zich in de
ruimte beweegt. Dan ligt de ruimtelijke component van de impulsvector natuurlijk
langs de positieve x-as en deze heeft per definitie de grootte px=mv.
Voor de wereldlijn geldt dat tan α = β = v/c ,
maar dan geldt ook dat tan α = px/p0 =β.
We kunnen daaruit concluderen dat de grootte van de
tijdcomponent p0 van de impulsvector gegeven wordt door
Hiermee is de ruimtetijd
impulsvector volledig bepaald zo lijkt het. Merk echter op dat alleen de
verhouding px/p0 is vastgelegd. Als we zowel p0
als px met dezelfde factor vermenigvuldigen blijft de
verhouding hetzelfde.