Hoofdstuk 6. Energie en impuls

6.2 Relativistische impulsvector

    • Afbeelding
    Figuur 6.2a Massa en impuls volgens Newton voor een stilstaand deeltje
    Figuur 6.2b Massa en impuls volgens Newton voor een bewegend deeltje

    We bekijken nu hoe de nieuwe impulsvector verandert onder de Galileï- dan wel Lorentz-transformaties. Om het verhaal zo duidelijk mogelijk te houden, zullen we de twee gevallen op analoge wijze behandelen.

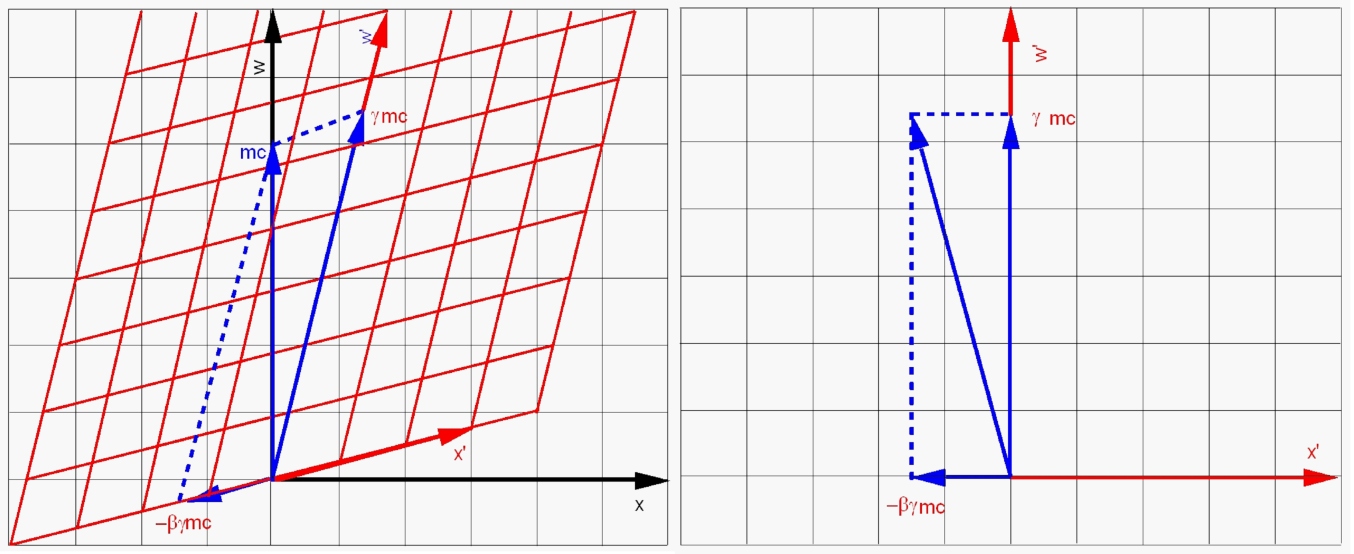
    We gaan uit van een stilstaand deeltje. Hierboven zie je hoe dat geval er volgens Newton (en Galileï) uitziet vanuit een bewegend stelsel. In figuur 6.2 staat de toestand van het deeltje afgebeeld in termen van de twee parameters die zijn bewegingstoestand (op een bepaald moment) beschrijven: de massa en impuls. Langs de verticale as staat mc, een massaparameter, en langs de horizontale as staat de impuls p x =−m⋅v=−β⋅mc . Een deeltje met massa m dat stilstaat (waarvoor geldt px = 0), wordt dan voorgesteld door een vector (pijl) langs de verticale as.

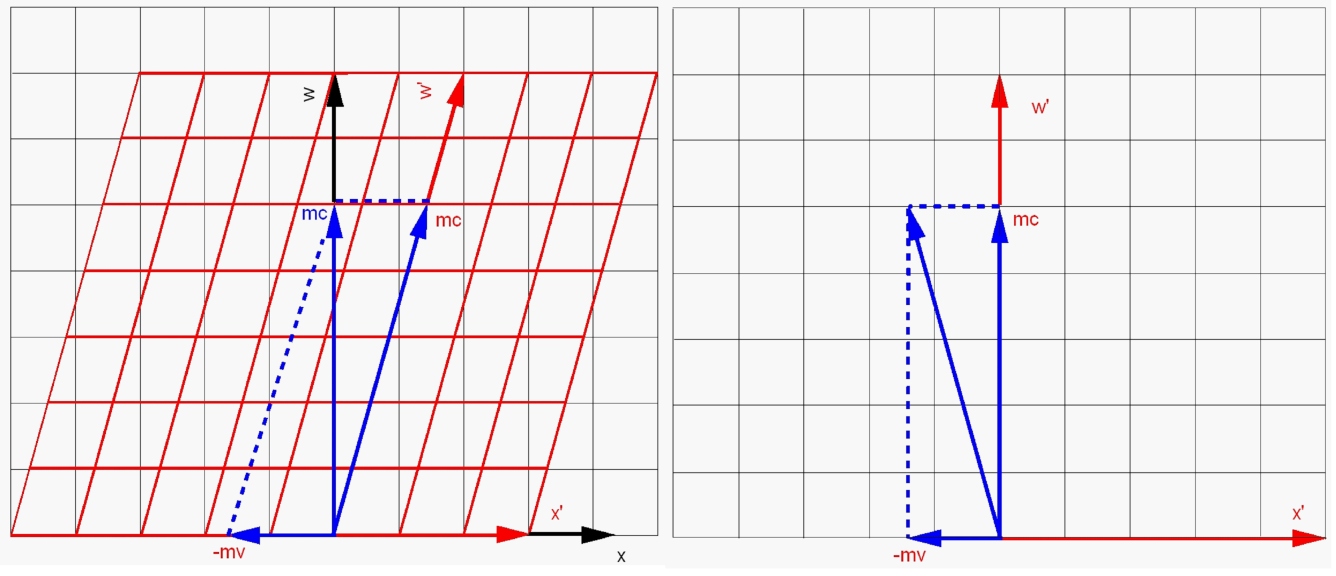
    In figuur 6.2a is ook een rood stelsel getekend, dat een newtoniaanse waarnemer voorstelt die zich voortbeweegt met snelheid v. In dat stelsel heeft het deeltje een snelheid -v en een impuls -mv. Merk op dat figuur 6.2a er precies zo uitziet als die voor de coördinaten w en x in figuur 2.10. Dat komt omdat die op exact dezelfde veranderen onder de Galileïtransformatie: voor een positievector in de ruimtetijd (w,x) weten we dat bij Newton w' = w en x'= x-vt = x- βw, terwijl voor de impulsvector in de ruimtetijd (mc, px) geldt dat

    (mc ) ′ =mc

    (omdat de massa niet verandert) en

    p ′ x = p x −m⋅v=−β⋅mc

    (omdat px=0). In figuur 6.2b zie je hoe de impulsvector er in het bewegende stelsel uitziet.

Relativistische impulsvector

De relativistische impulsvector voor een deeltje met massa m en snelheid v heeft 'ruimtetijd' componenten

( p 0 , p x )=(γmc,βγmc)=( mc 1− v 2 / c 2 , mv 1− v 2 / c 2 )

Waarin β = v/c. De uitdrukking verschilt van die van Newton door de extra relativistische snelheidsfactor γ.

Een foton of lichtdeeltje verplaatst zich per definitie altijd met de lichtsnelheid. De ruimtetijdimpuls ervan ligt in de richting van de bijbehorende wereldlijn en heeft daardoor voor alle waarnemers een even grote ruimte- als tijdscomponent. De fysica van het elektromagnetisme leert dat we ook aan licht een energie E en impuls p kunnen toekennen, die een constante verhouding hebben van

E p =c

gelijk dus aan de lichtsnelheid. Die verhouding is daardoor hetzelfde voor alle waarnemers. Hieruit volgt dat de tijdscomponent van de impulsvector van een foton gelijk moet zijn aan E/c.

Een foton gaat met de lichtsnelheid, maar kan wel een welbepaalde eindige impuls (en energie) hebben, in tegenstelling tot de deeltjes die we hiervoor bespraken. Materiedeeltjes zouden bij de lichtsnelheid een oneindige energie en impuls bezitten, hetgeen onmogelijk is - dit verklaart dat zij de lichtsnelheid nooit bereiken. In de figuur 6.4 is zo'n eindige 'energie-impulsvector' van een foton weergegeven. Merk op dat de componenten van de vector in de verschillende bewegende stelsels allemaal op een rechte lijn loodrecht op de wereldlijn terechtkomen.

In tegenstelling tot een massief deeltje, waarvan de impuls onbeperkt toeneemt, gedraagt licht zich keurig. Als we het foton willen interpreteren als een deeltje waarvan beide impulscomponenten een eindige waarde houden terwijl γ oneindig groot is, kan dat alleen als we eisen dat de fotonmassa naar nul gaat, zodat γmc kan worden vervangen door de energie E/c. We moeten het foton als een massaloos deeltje opvatten.

Ook het graviton, waarvan Einstein het bestaan voorspelde in zijn algemene relativiteitstheorie, maar waarvan het bestaan nog steeds niet is aangetoond, is zo'n massaloos deeltje. Algemeen geldt dat alle deeltjes die met de lichtsnelheid bewegen massaloos zijn, en omgekeerd!

Afbeelding
Figuur 6.4 Impuls en energie van een foton