Gebonden toestanden

De continuïteitsvergelijking voor de energie (2.6) kan niet analytische worden opgelost. Het vinden van (numerieke of grafische) oplossingen wordt vereenvoudigd door over te gaan op dimensieloze variabelen $u = κ L / π$ en $v = k L / π$ . Als referentie voor de energie gebruiken we de nulpuntsenergie $E_{1} = π {}^{2}/ γ L^{2}$ van het deeltje-in-een-doos probleem; zie (2.3). Uit deze definities volgt

Daarmee herschrijven we de vergelijking (2.6) als

De cot-functie is periodiek met periode $π$ . Voor ieder periode kunnen we (grafisch of numeriek) een oplossing $v_{n}$ vinden, met $n = 1,2,..$ , mits $v_{n} \leq u_{0}$ . De oplossingen liggen in het interval $2 n - 1 \leq 2 v_{n} \leq 2 n \leq u_{0}^{}$ .
De parameter $u_{0}$ is een maat voor de diepte van de potentiaalput en dus het aantal mogelijke gebonden toestanden. Het aantal gebonden toestanden wordt gegeven door het grootste gehele getal $N$ kleiner dan $u_{0} + 1 / 2$ .

Als $u_{0} ≫ 1$ dan is het aantal gebonden toestanden groot. De energieën van de laagste energieniveaus zijn dan bijna gelijk aan die van een deeltje-in-een-doos: $v_{1} \approx 1, v_{2} \approx 2,..$ .
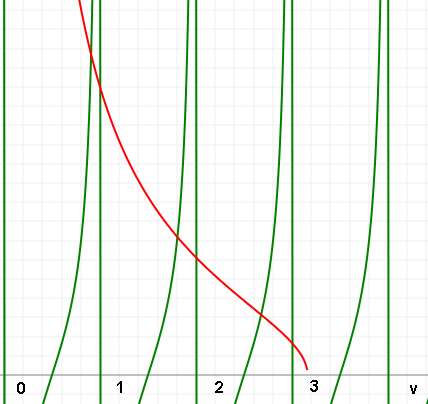
Als $U_{0}$ slechts enkele malen groter is dan $E_{1}$ zijn er maar een paar gebonden toestanden. Bijvoorbeeld, voor $u_{0}^{2} = 10$ zijn er drie gebonden toestanden met $v_{1} = 0,90736$ , $v_{2} = 1,80646$ en $v_{3} = 2,67841$ ; zie figuur.