Synopsis Quantummechanica II

Quantumdeeltje-in-een-potentiaalput

We beschouwen een model-potentiaal die een oneindige ondoordringbare wand bevat ter plaatse $x = 0$ en een eindig hoge wand ter plaatse van $x = L$ , zoals geschetst in de figuur. De potentiaalfunctie is nul voor $x$ tussen 0 en $L$ , oneindig voor negatieve $x$ , en gelijk aan een constante, zeg $U_{0}$ , voor $x$ groter dan $L$ :

2.4

V (x) = {\begin{cases} \infty x < 0 \\ 0 0 \leq x \leq L \\ U_{0} x > L \end{cases}

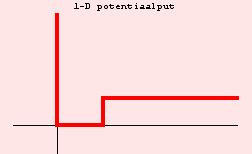
In de put is $V (x) = 0$ . Daar heeft de golffunctie de vorm van een sinusfunctie $ψ_{1} (x) = A \sin k \cdot x$ met golfgetal $k = \sqrt{γ E}$ . Buiten de put $x > L$ zijn er twee mogelijkheden, zie (1.17): voor $E > U_{0}$ is de oplossing van de 1-dim Schrödingervergelijking een sinusfunctie, maar voor $E < U_{0}$ is de oplossing een afnemende exponentiële functie $ψ_{2} (x) = B \exp - κ \cdot x$ met dempingscoëfficiënt $κ = \sqrt{γ (U_{0} - E})$ . Hieronder bekijken we deze laatste oplossing nader.

Golffuncties moeten continu en differentieerbaar zijn, d.w.z. de golffuncties $ψ_{1}, ψ_{2}$ en de afgeleiden daarvan moeten continu zijn op de rand $L$ . Hieruit volgen de condities:

2.5

A \sin k L = B e^{- κ L} k A \cos k L = - κ B e^{- κ L}

Delen op elkaar geeft de continuïteitsconditie

2.6

- k \cot k L = κ

Via de energieafhankelijkheid van het golfgetal $k$ en de dempingscoëfficiënt $κ$ is vergelijking (2.6) een conditie op de energie.
Het glad aan elkaar laten sluiten van de golffuncties op de rand van de put is alleen mogelijk voor specifieke energiewaarden die voldoen aan de continuïteitsconditie (2.6). De energieniveaus zijn discreet voor $E < U_{0}$ en de eigenfuncties representeren gebonden toestanden; zie volgende pagina.