Synopsis Quantummechanica II

Harmonische eigenfuncties

Het vinden van de eigenwaarden en eigenfuncties uit de Schrödingervergelijking (2.14) wordt vereenvoudigd door de plaats-coördinaat te schalen met de karakteristieke debroglielengte $λ_{0} = \sqrt{ℏ / m ω}$ en de energie met de nulpuntsenergie: $ε_{n} = E_{n} / E_{0}$ . Na deze herdefinities van de plaats-coördinaat en de energie, en met de relaties: $λ_{0}^{2} \cdot E_{0} \cdot γ = 1$ en $C \cdot λ_{0}^{2} / 2 E_{0} = 1$ , krijgt de Schrödingervergelijking (2.14) de dimensieloze vorm

2.16

(- \frac{d^{2}}{d x^{2}} + x^{2} - ε_{n}) ψ_{n} (x) = 0

Het is eenvoudig na te gaan dat $ψ_{0} (x) = \exp (- x^{2} / 2)$ een oplossing is met $ε_{0} = 1$ . Dit is de grondtoestand.

De hogere eigenfuncties worden gevonden door te schrijven

2.17

ψ_{n} (x) = H_{n} (x) e^{- x^{2} / 2}

Dan reduceert de 1-dim Schrödingervergelijking tot de differentiaalvergelijking

2.18

[\frac{d^{2}}{d x^{2}} - 2 x \frac{d}{d x} + ε_{n} - 1] H_{n} (x) = 0

Deze differentiaalvergelijking heeft, voor de waarden $ε_{n} - 1 = 2 n$ , de uit de wiskunde bekende Hermite polynomen $H_{n} (x)$ van de graad $n$ als oplossing. De laagste oplossingen zijn:

2.19a

H_{0} (x) = 1

2.19b

H_{1} (x) = 2 x

2.19c

H_{2} (x) = 4 x^{2} - 12 x

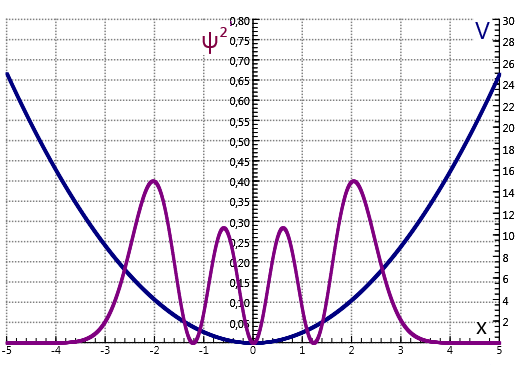
Alleen voor gehele getallen $ε_{n} = 2 n + 1$ heeft de Schrödingervergelijking (2.16) fysisch aanvaardbare oplossingen (d.w.z. oplossingen die eindig blijven en naar nul gaan ver van de oorsprong). De figuur is getekend voor $n = 3$ .
Daarmee is het spectrum (2.15) van de quantum harmonische oscillator met bijbehorende eigenfuncties (2.17) vastgelegd.