Synopsis Quantummechanica II

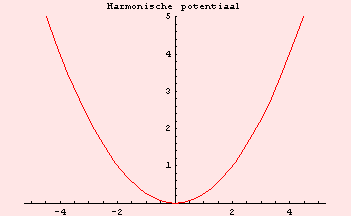
Harmonische oscillator

  • Een harmonische potentiaal komt in veel toepassingen voor. Het is de natuurlijke benadering voor de beschrijving van trillingen in een systeem in evenwicht.
  • De energietoestanden van de quantum harmonische oscillator zijn evenredig met de trillingsfrequentie van een klassiek massa-veersysteem.

Voor systemen met veel deeltjes is het vaak een goede benadering te veronderstellen dat trillingen rond de evenwichtspositie beschreven worden door een harmonische potentiaal, alsof de trillende deeltjes een massa zijn aan een veer met veerconstante C :

2.13

V(x)= 1 2 C⋅ x 2

De 1-dim Schrödingervergelijking voor de quantum harmonische oscillator wordt gegeven door

2.14

d 2 ψ(x) d x 2 +γ( E− 1 2 C⋅ x 2 )ψ(x)=0

met de afkorting γ=2m/ ℏ 2 . Bijzonder is dat voor dit geval de Schrödingervergelijking analytisch kan worden opgelost. De discrete energiewaarden worden gevonden als

2.15

E n =(2n+1) E 0     E 0 = 1 2 ℏω

met n=0,1,2,...  en ω= C/m de hoekfrequentie van een klassiek massa-veersysteem; zie volgende pagina voor de wiskundige afleiding.

  • De energieniveaus van de harmonische oscillator zijn veelvouden van ℏω , zoals Max Planck al veronderstelde in 1900.