Synopsis Quantummechanica II

Waterstofatoom

  • Net als bij een quantumdeeltje in een put zijn de energietoestanden van een elektron in een coulombpotentiaal gequantiseerd.
  • De energietoestanden berekend met dit model voor het waterstofatoom zijn omgekeerd evenredig met het kwadraat van het quantumgetal n=1,2,3,.. .

Het elektron en het proton in het waterstofatoom ondervinden de aantrekking van de coulombkracht afhankelijk van hun afstand r

2.20

V(r)=− e 2 4π ε 0 r

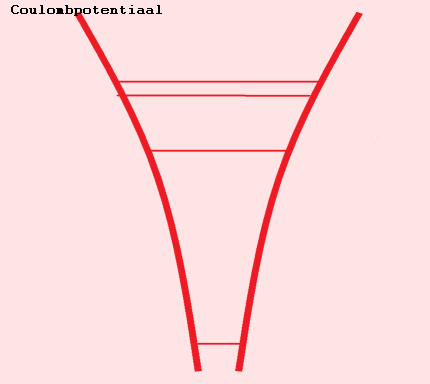
Voor dit geval is de 1-dimensionale (radiële) Schrödingervergelijking:

2.21

d 2 ψ(r) d r 2 +γ( E+ e 2 4π ε 0 r )ψ(r)=0

Hierin zijn ε 0 en γ=2m/ ℏ 2 constanten en is e=1,6022 ×  10 − 19  C de lading en m=9,1× 10 −31  kg de (gereduceerde) massa van het elektron.

Op de volgende pagina wordt berekend dat de energieniveaus gegeven worden door

2.22

E n =− R y n 2    n=1,2,3,..
  • De constante R y = ℏ 2 /2m a 0 2 =13,61 eV is de rydberg-energie, met a 0 de bohrstraal. Hoe groter het getal n , des te dichter liggen de energieniveaus bij elkaar.
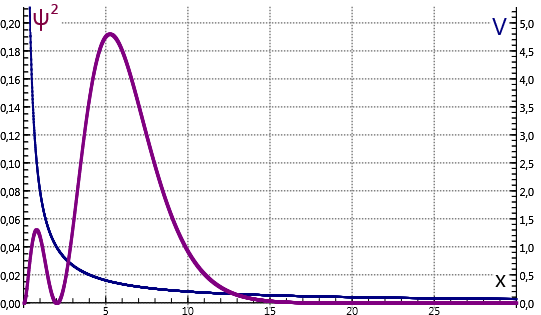
  • De kans om het elektron op een afstand r van de kern aan te treffen wordt bepaald door het kwadraat van de golffunctie | ψ(r) | 2 . In de grondtoestand ligt het maximum bij de bohrstraal a 0 =4π ε 0 ℏ 2 /m e 2 =5,29⋅ 10 −2  nm . De figuur is is getekend voor n=2.