Synopsis Quantummechanica II

Quantumdeeltje-in-een-doos

Het begrip 1-dimensionale doos wordt gedefinieerd als een potentiaalput die twee, voor een deeltje ondoordringbare, wanden bevat ter plaatse van $x = 0$ en $x = L$ , zoals geschetst in de figuur. Als de wanden oneindig hoog zijn spreekt men van een doos. De potentiaalfunctie is dan

2.1

V (x) = {\begin{cases} \infty x < 0 \\ 0 0 \leq x \leq L \\ \infty x > L \end{cases}

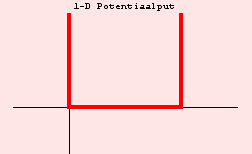
Bij het zoeken naar geschikte oplossingen van de Schrödingervergelijking voor deze situatie kan allereerst geconcludeerd worden dat $ψ (x) = 0$ buiten de doos omdat er geen kans is het deeltje daar aan te treffen. Binnen de doos is de potentiaalfunctie nul en luidt de Schrödingervergelijking:

2.2

- \frac{h^{2}}{8 m π^{2}} \frac{d^{2} ψ (x)}{d x^{2}} = E ψ (x)

De oplossing van de 1-dim Schrödingervergelijking is daar een sinusfunctie $ψ (x) = A \sin (k \cdot x)$ met amplitude $A$ en golfgetal $k = \sqrt{γ E}$ . De afkorting $γ : = 2 m / ℏ^{2}$ is een constante.

De golffunctie moet voldoen aan de randvoorwaarden $ψ (0) = 0, ψ (L) = 0$ , d.w.z. $k \cdot L = π \cdot n, n = 1,2,3,..$ . Met $p = ℏ k$ en $E = p^{2} / 2 m$ volgen de toegestane energiewaarden hieruit als:

2.3

E_{n} = E_{1} \cdot n {}^{2} E_{1} = \frac{π^{2}}{γ \cdot L^{2}} = \frac{h^{2}}{8 m \cdot L^{2}}

De laagste energietoestand met energie $E_{1}$ heet de grondtoestand. De energie van een deeltje in een doos kan niet nul zijn omdat dan ook de golffunctie nul moet zijn. Algemeen geldt dat een quantumdeeltje in een gebonden toestand altijd een zekere nulpuntsenergie heeft, ook als de temperatuur nul kelvin is.
Als de put een nano-afmeting heeft, bijvoorbeeld $L = 2 nm$ , een typische waarde voor een quantum dot, en de massa is die van een elektron, dan is de energie van de grondtoestand $E_{1} = 1,5 \cdot 10^{- 20} J$ .
In SI-eenheden is dit een onhandig klein getal. Daarom is het gebruikelijk om de energie van atomaire processen uit te drukken in elektronvolt: $E_{1} ≃ 0,1 eV$ .