subsectie asymmetrische put

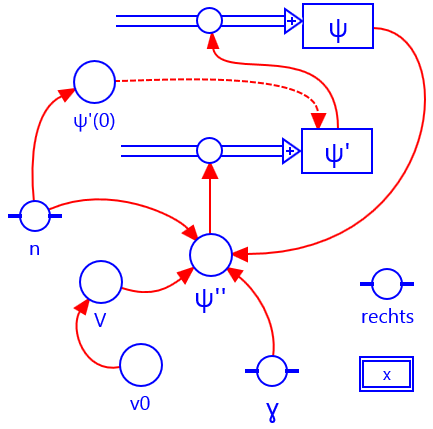
In dit model bevindt een quantumdeeltje zich in een asymmetrische 1-dimensionale put met eindige diepte. De potentiaal is $V (x) = \infty$ voor $ x < 0 $ en $V (x) = V_{0}$ voor $x > L$ . In de put is de potentiële energie $V (x) = 0$ . Daar heeft de golffunctie $ψ_{1} (x)$ de vorm van een sinus met golfgetal $k = \sqrt{γ E}$ . Buiten de put is de oplossing van de 1-dim Schrödingervergelijking een exponentiële functie $ψ_{2} (x)$ met dempingscoëfficiënt $κ = \sqrt{γ (V_{0} - E)}$ .
De toegelaten energiewaarden kunnen numeriek berekend worden uit de conditie dat de golffunctie en de afgeleide continu zijn op de rand: $ψ_{1} (L) = ψ_{2} (L)$ en $ψ'_{1} (L) = ψ'_{2} (L)$ .¹

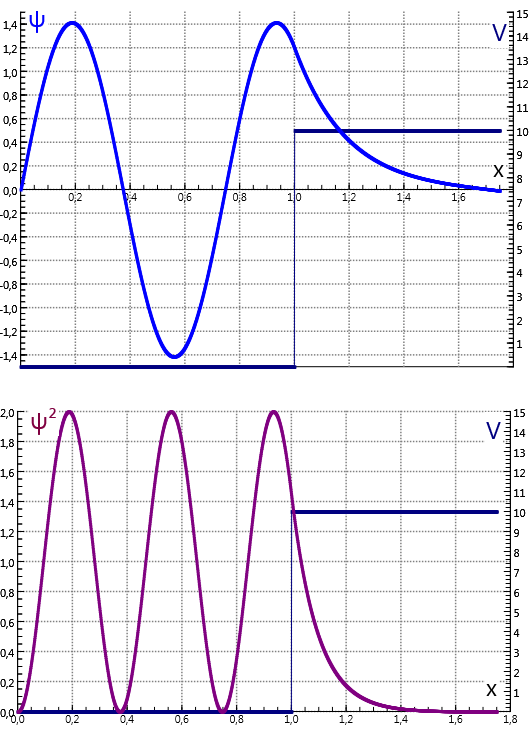
In het voorbeeld hieronder worden de eigenwaarden gevonden door te zoeken naar golffuncties die eindig blijven voor bepaalde waarden van $E$ . De parameters zijn dezelfde als die in model 7.2 en we schrijven voor de energie $E = E_{1} \cdot n^{2}$ met $E_{1}$ de energie van de grondtoestand zoals gevonden in 7.2; $n$ is hier een variabele. Door deze variabele te variëren rond de waarde 1 wordt de grondtoestand voor de ondiepe put gevonden: $n_{1} = 0,90736$ . Op dezelfde wijze kunnen ook de eerste aangeslagen toestanden $n_{2}, n_{3}$ berekend worden, mits $E - V_{0} < 0$ .

De modelregels worden vereenvoudigd door over te gaan op dimensieloze variabelen. Dan blijkt dat de relatieve potentiaal $v_{0}$ de bepalende parameter is in het probleem.

Formules uit Binas:

\frac{d^{2} ψ (x)}{d x^{2}} + γ (E - V (x)) \cdot ψ (x) = 0

\begin{array}{l} E = \frac{1}{2} m \cdot v^{2} + V (x) \\ γ = 8 π^{2} \cdot m / h^{2} \end{array}

Differentievergelijkingen:

\begin{array}{l} ψ^{″} = - γ \cdot (E - V) \cdot ψ \\ Δ ψ^{'} = ψ^{″} \cdot Δ x \\ Δ ψ = ψ^{'} \cdot Δ x \end{array}

Oplossing $V = 0$ :

\begin{array}{l} ψ_{1} (x) = A \sin k \cdot x \\ k = \sqrt{γ E} \end{array}

Oplossing $V = V_{0}$ :

\begin{array}{l} ψ_{2} (x) = F \exp - κ \cdot x \\ κ = \sqrt{γ (V_{0} - E)} \end{array}

Dimensieloze variabelen:

\begin{array}{l} x \to L \cdot x \\ ψ^{″} \to L^{- 2} \cdot ψ^{″} \\ n^{2} = E / E_{1} \\ v_{0} = V_{0} / E_{1} \\ γ \to L^{2} \cdot E_{1} \cdot γ = π^{2} \end{array}

Modelregels

\begin{array}{l} 0 \leq x \\ Als x > 1 \\ Dan v = v_{0} \\ Anders v = 0 \\ Eindals \\ ψ^{″} = - γ \cdot (n^{2} - v) \cdot ψ \\ ψ^{'} = ψ^{'} + ψ^{″} \cdot d x \\ ψ = ψ + ψ^{'} \cdot d x \\ x = x + d x \end{array}

Grafisch model