subsectie quantumdeeltje-in-een-doosje

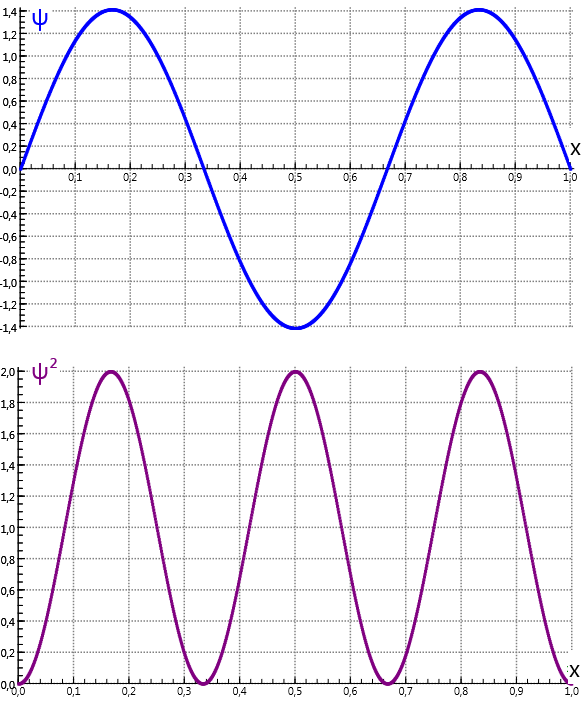
Beschouwd wordt een quantumdeeltje opgesloten in een 1-dimensionale diepe put met potentiaal $V (x) = \infty$ voor $x < 0, x > L$ . In de put is de potentiële energie $V (x) = 0$ . Daar is de oplossing van de 1-dim Schrödingervergelijking een sinus-functie.

Deze golffunctie $ψ (x)$ moet voldoen aan de randvoorwaarde $ψ (0) = 0, ψ (L) = 0$ , d.w.z. $k \cdot L = π \cdot n, n = 1, 2, 3, ..$ . De toegestane energiewaarden volgen hieruit als:¹ $E_{n} = E_{1} \cdot n^{2} E_{1} = \frac{π^{2}}{γ \cdot L^{2}} = \frac{h^{2}}{8 m \cdot L^{2}}$ Als de put een nano-afmeting heeft, bijvoorbeeld $L = 2 nm$ , een typische waarde voor een quantum dot, en de massa is die van een elektron, dan is de energie van de grondtoestand $E_{1} = 1, 5 \cdot 10^{- 20} J$ . In SI-eenheden is dit een onhandig klein getal. Daarom is het gebruikelijk om de energie van atomaire processen uit te drukken in elektronvolt: $E_{1} ≅ 0, 1 eV$ .

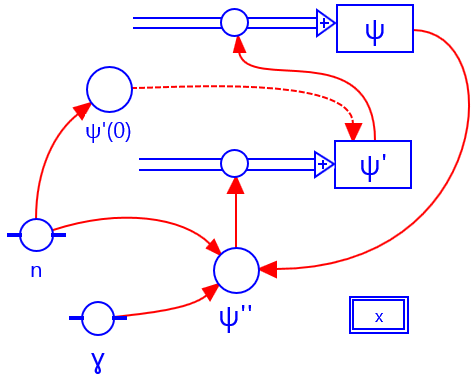
Hieronder wordt dit model doorgerekend. De conditie dat de golffunctie nul moet zijn op de rand is verdisconteerd in de startwaarde van de energie. In de modelregels zijn de variabelen dimensieloos na schaling met de lengte $L$ en de energie $E_{1}$ .

Formules uit Binas:

\frac{d^{2} ψ (x)}{d x^{2}} + γ (E - V (x)) \cdot ψ (x) = 0

\begin{array}{l} E = \frac{1}{2} m \cdot v^{2} + V (x) \\ γ = 8 π^{2} \cdot m / h^{2} \end{array}

Differentievergelijking:

\begin{array}{l} ψ^{″} = - γ \cdot (E - V) \cdot ψ \\ Δ ψ^{'} = ψ^{″} \cdot Δ x \\ Δ ψ = ψ^{'} \cdot Δ x \end{array}

Oplossing $V = 0$ :

ψ (x) = A \sin k \cdot x k = \sqrt{γ E}

Dimensieloze variabelen:

\begin{array}{l} x \to L \cdot x \\ ψ^{″} \to L^{- 2} \cdot ψ^{″} \\ n^{2} = E / E_{1} \\ γ \to L^{2} \cdot E_{1} \cdot γ = π^{2} \end{array}

Modelregels

\begin{array}{l} 0 \leq x \leq 1 \\ ψ^{″} = - γ \cdot n^{2} \cdot ψ \\ ψ^{'} = ψ^{'} + ψ^{″} \cdot d x \\ ψ = ψ + ψ^{'} \cdot d x \\ x = x + d x \end{array}

Grafisch model