subsectie symmetrische put

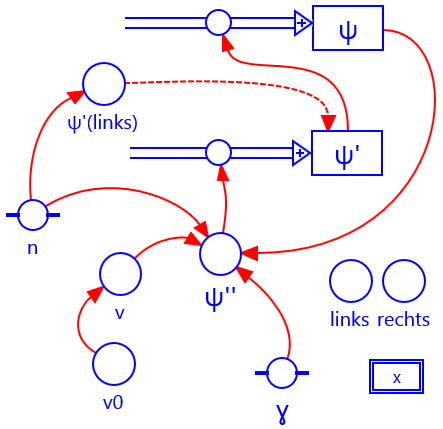
Als variant van model 7.3 wordt een quantumdeeltje beschouwd in een symmetrische 1-dimensionale put met twee eindige wanden. De potentiaal is $V (x) = V_{0}$ voor $| x | > L / 2$ . In de put $| x | < L / 2$ is de potentiële energie $V (x) = 0$ . Daar is de golffunctie $ψ_{2} (x)$ een lineaire combinatie van een sin- en een cos-functie, met twee constanten A en B die bepaald worden uit de randcondities op de wanden van de put en de normering. Buiten de put is de oplossing een exponentiële functie $ψ_{1,3} (x)$ met te bepalen constanten $F$ en $G$ .

De toegelaten energiewaarden kunnen numeriek berekend worden uit de condities dat de golffunctie en de afgeleide continu zijn op de randen:¹ $ψ_{1} (- L / 2) = ψ_{2} (- L / 2)$ , $ψ_{1}^{'} (- L / 2) = ψ_{2}^{'} (- L / 2)$ en idem voor $ψ_{2,3}$ bij $L / 2$ .

In het voorbeeld hieronder worden de eigenwaarden berekend met de modelregels. Deze regels kunnen vereenvoudigd worden door over te gaan op dimensieloze variabelen zoals bij model 7.3. $E_{1}$ is de energie van de grondtoestand van model 7.2 en de waarden voor de parameters zijn dezelfde als die in model 7.3.

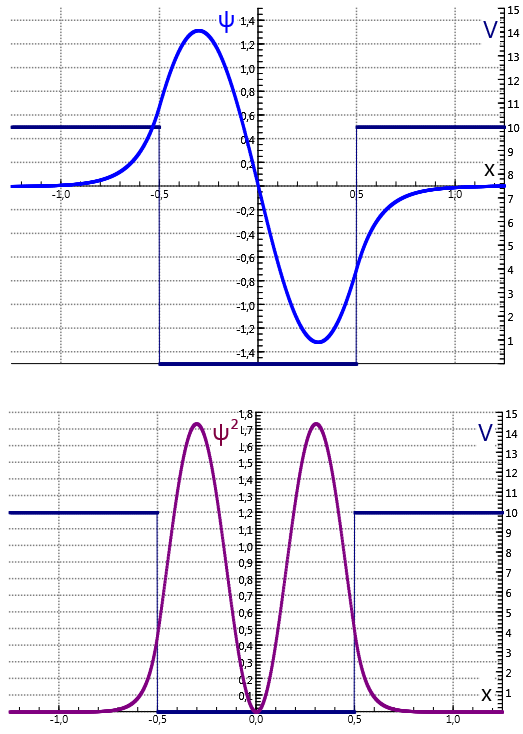
De discrete eigenwaarden worden gevonden door te zoeken naar oplossingen die eindig blijven voor bepaalde waarden van $n$ . Door de variabele $n$ te variëren rond de waarde 1,.. wordt de grondtoestand van de symmetrische put gevonden: $n_{1} = 0,83077$ . Op dezelfde wijze kan ook de eerste aangeslagen toestand $n_{2}$ berekend worden, mits $E - V_{0} < 0$ .

Formules uit Binas:

\frac{d^{2} ψ (x)}{d x^{2}} + γ (E - V (x)) \cdot ψ (x) = 0

\begin{array}{l} E = \frac{1}{2} m \cdot v^{2} + V (x) \\ γ = 8 π^{2} \cdot m / h^{2} \end{array}

Differentievergelijkingen:

\begin{array}{l} ψ^{″} = - γ \cdot (E - V) \cdot ψ \\ Δ ψ^{'} = ψ^{″} \cdot Δ x \\ Δ ψ = ψ^{'} \cdot Δ x \end{array}

Oplossing $x < - L / 2$ :

\begin{array}{l} ψ_{1} (x) = G \exp κ \cdot x \\ κ = \sqrt{γ (V_{0} - E)} \end{array}

Oplossing $| x | < L / 2$ :

\begin{array}{l} ψ_{2} (x) = A \sin k \cdot x + B \cos k \cdot x \\ k = \sqrt{γ E} \end{array}

Oplossing $| x | < L / 2$ :

\begin{array}{l} ψ_{3} (x) = F \exp - κ \cdot x \\ κ = \sqrt{γ (V_{0} - E)} \end{array}

Dimensieloze variabelen:

\begin{array}{l} x \to L \cdot x \\ ψ^{″} \to L^{- 2} \cdot ψ^{″} \\ n^{2} = E / E_{1} \\ v_{0} = V_{0} / E_{1} \\ γ \to L^{2} \cdot E_{1} \cdot γ = π^{2} \end{array}

Modelregels

\begin{array}{l} Als x < - 0, 5 of x > 0, 5 \\ Dan v = v_{0} \\ Anders v = 0 \\ Eindals \\ Als (links < x) en (x < rechts) \\ Dan \\ ψ^{″} = - γ \cdot (n^{2} - v) \cdot ψ \\ d ψ^{'} = ψ^{″} \cdot d x \\ d ψ = ψ^{'} \cdot d x \\ Anders \\ d ψ^{'} = 0 \\ d ψ = 0 \\ EindAls \\ ψ^{'} = ψ^{'} + d ψ^{'} \\ ψ = ψ + d ψ \\ x = x + d x \end{array}

Grafisch model

Startwaarden

\begin{array}{l} links = - 5 / 4 \\ rechts = 5 / 4 \\ n_{1} = 0,83077 \\ n_{2} = 1,65044 \\ n_{3} = 2,43928 \\ n = n_{2} \\ γ = π^{2} \\ v_{0} = 10 \\ ψ^{'} (links) = 1 / (- 1000 + 2500 \cdot n - 750 \cdot n^{2}) \\ \cdot 1,1 \cdot n^{2} \cdot \sqrt{2 \cdot n \cdot π} \\ ψ^{'} = ψ^{'} (links) \\ ψ = 0 \\ x = links \\ d x = 0,001 \end{array}