subsectie quantum-tunneling

Quantumdeeltjes kunnen potentiaal-barrières passeren die volgens de klassieke mechanica ondoordringbaar zijn. De verklaring voor dit effect van tunneling is het feit dat de golffunctie bij een eindige energiebarrière niet nul is maar exponentieel afneemt; zie modellen 7.3-6.

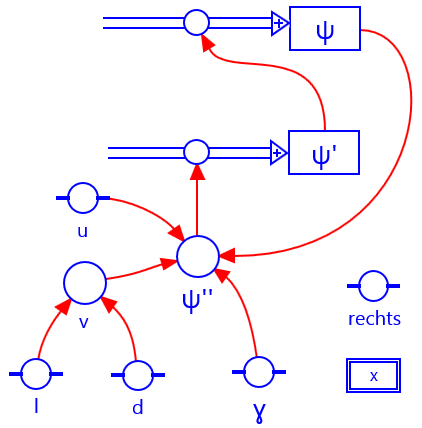
Als eenvoudig model, voor bijvoorbeeld een scanning tunneling microscoop (STM)^6,10, wordt een energie-barrière met hoogte $V = V_{0}$ en breedte $D$ beschouwd. In het gebied $x < L$ links en het gebied $L + D < x$ rechts van de barrière kan een quantumdeeltje vrij bewegen met energie $E > 0$ . In die gebieden zijn de golffuncties $ψ_{1, 3}$ lineaire combinaties van sin- en cos-functies. In de barrière geldt $E < V_{0}$ en is de oplossing een exponentiële functie $ψ_{2}$ . De normeringsconstanten worden vastgelegd door de conditie dat de golffunctie en de afgeleide continu zijn op de randen.²

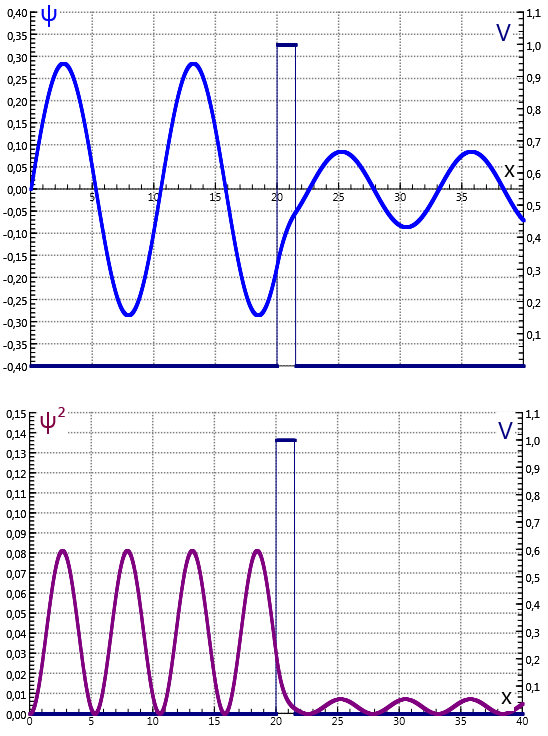
De conclusie is dat de waarschijnlijkheid $| ψ_{3} |^{2}$ om het deeltje rechts van de potentiaalbarrière aan te treffen een eindige waarde heeft. De transmissiecoëfficiënt die de kans geeft dat een deeltje naar buiten tunnelt wordt voor $κ \cdot D ≫ 1$ bij benadering gegeven door³ $T ≃ \frac{| ψ_{2} (L + D) |^{2}}{| ψ_{2} (L) |^{2}} = \exp - 2 κ \cdot D$ Een hogere en bredere barrière betekent een (veel) kleinere kans.

In het voorbeeld hieronder wordt dit eenvoudige model doorgerekend. Links en rechts van de barrière wordt het quantumdeeltje als vrij beschouwd $E > 0$ , maar in de barrière geldt $E < V_{0}$ . In de modelregels wordt de coördinaat geschaald met de lengte $x_{0} = \sqrt{1 / γ \cdot V_{0}}$ die een maat is voor de afstand waarover de golffunctie vervalt in de barrière; de relevante energieën worden geschaald met de hoogte van de barrière $V_{0}$ .

Formules uit Binas:

\frac{d^{2} ψ (x)}{d x^{2}} + γ (E - V (x)) \cdot ψ (x) = 0

\begin{array}{l} E = \frac{1}{2} m \cdot v^{2} + V (x) \\ γ = 8 π^{2} \cdot m / h^{2} \end{array}

Differentievergelijkingen:

\begin{array}{l} ψ^{″} = - γ \cdot (E - V) \cdot ψ \\ Δ ψ^{'} = ψ^{″} \cdot Δ x \\ Δ ψ = ψ^{'} \cdot Δ x \end{array}

Oplossing $x < L$ :

\begin{array}{l} ψ_{1} (x) = A \sin k \cdot x + B \cos k \cdot x \\ k = \sqrt{γ E} \end{array}

Oplossing $L < x < L + D$ :

\begin{array}{l} ψ_{2} (x) = F \exp - κ \cdot x \\ κ = \sqrt{γ (V_{0} - E)} \end{array}

Oplossing $x > L + D$ :

\begin{array}{l} ψ_{3} (x) = G \sin k \cdot x + H \cos k \cdot x \\ k = \sqrt{γ E} \end{array}

Dimensieloze variabelen:

\begin{array}{l} x \to x_{0} \cdot x x_{0} = 1 / \sqrt{γ V_{0}} \\ ψ^{″} \to x_{0}^{- 2} \cdot ψ^{″} \\ l = L / x_{0} \\ d = D / x_{0} \\ u = E / V_{0} \\ v = V / V_{0} \\ γ \to x_{0}^{2} \cdot V_{0} \cdot γ = 1 \end{array}

Modelregels

\begin{array}{l} 0 \leq x \leq rechts \\ Als (x > l) en (x < l + d) \\ Dan v = 1 \\ Anders v = 0 \\ EindAls \\ ψ^{″} = - γ \cdot (u - v) \cdot ψ \\ ψ^{'} = ψ^{'} + ψ^{″} \cdot d x \\ ψ = ψ + ψ^{'} \cdot d x \\ x = x + d x \end{array}

Grafisch model