subsectie waterstofatoom

Het elektron en het proton in een waterstofatoom ondervinden de aantrekking van de coulombkracht. Net als bij een quantumdeeltje in een put zijn de energietoestanden van het waterstof-elektron gequantiseerd:¹ $E_{n} = - \frac{R_{y}}{n^{2}} n = 1, 2, 3...$ met $R_{y} = 13, 61 eV$ de rydberg-energie. Hoe groter $n$ des te dichter liggen de energieniveaus bij elkaar.

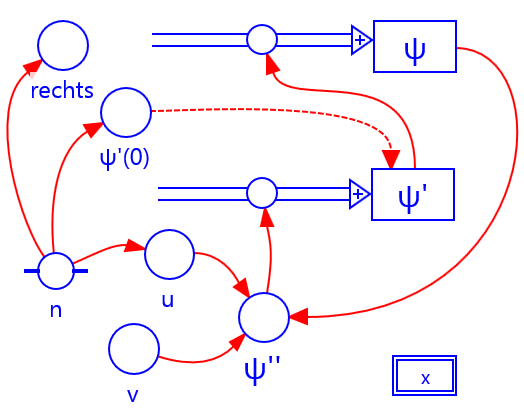
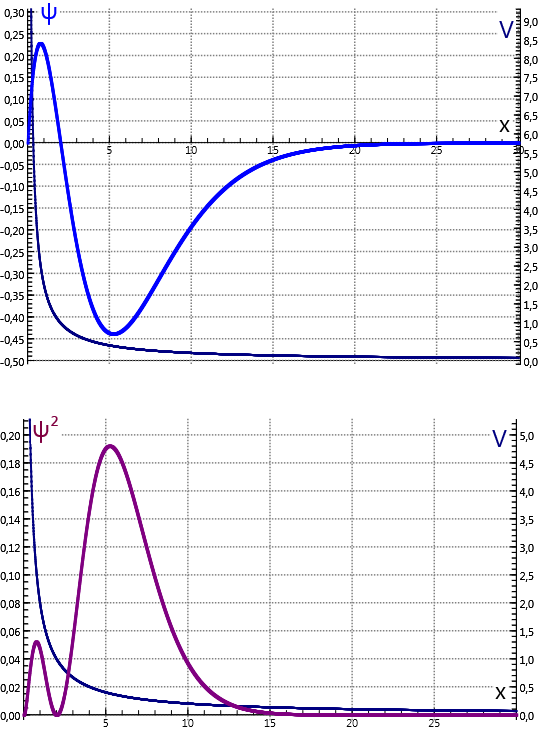
In de quantummechanica wordt het waterstof-elektron beschreven met een golffunctie $ψ$ . De kans om het elektron op een afstand $r$ van de kern aan te treffen wordt gegeven door het kwadraat van de golffunctie ${| ψ (r) |}^{2}$ . In de grondtoestand ligt het maximum bij de bohrstraal $a_{0} ≃ 5, 29 \cdot 10^{- 2} nm$ , zoals in het voorbeeld berekend wordt.

Ter vereenvoudiging van de modelregels worden dimensieloze variabelen geïntroduceerd.

Formules uit Binas:

\frac{d^{2} ψ (r)}{d r^{2}} + γ (E + f \frac{e^{2}}{r}) \cdot ψ (r) = 0

\begin{array}{l} f = 1 / 4 π ε_{0} \\ γ = 8 π^{2} \cdot m / h^{2} \end{array}

Differentievergelijkingen:

\begin{array}{l} ψ^{″} = - γ \cdot (E + f \cdot e^{2} / r) \cdot ψ \\ Δ ψ^{'} = ψ^{″} \cdot Δ r \\ Δ ψ = ψ^{'} \cdot Δ r \end{array}

Waterstofatoom:

\begin{array}{l} a_{0} = h^{2} / (4 π^{2} f \cdot e^{2} \cdot m_{e}) \\ E_{1} = - f \cdot e^{2} / 2 a_{0} = - R_{y} \\ a_{0}^{2} \cdot R_{y} \cdot γ = 1 \end{array}

Dimensieloze variabelen:

\begin{array}{l} x = r / a_{0} \\ u^{2} = - E / R_{y} \end{array}

Modelregels

\begin{array}{l} 0 < x \leq rechts \\ v = 2 / x \\ ψ^{″} = (u^{2} - v) \cdot ψ \\ ψ^{'} = ψ^{'} + ψ^{″} \cdot d x \\ ψ = ψ + ψ^{'} \cdot d x \\ x = x + d x \end{array}

Grafisch model