Wat klopt hiervan met de werkelijkheid, en wat niet?
In figuur 4.8 zie je de echte energieniveaus van het elektron in een waterstofatoom, zoals die volgen uit metingen van het absorptie- en emissiespectrum.
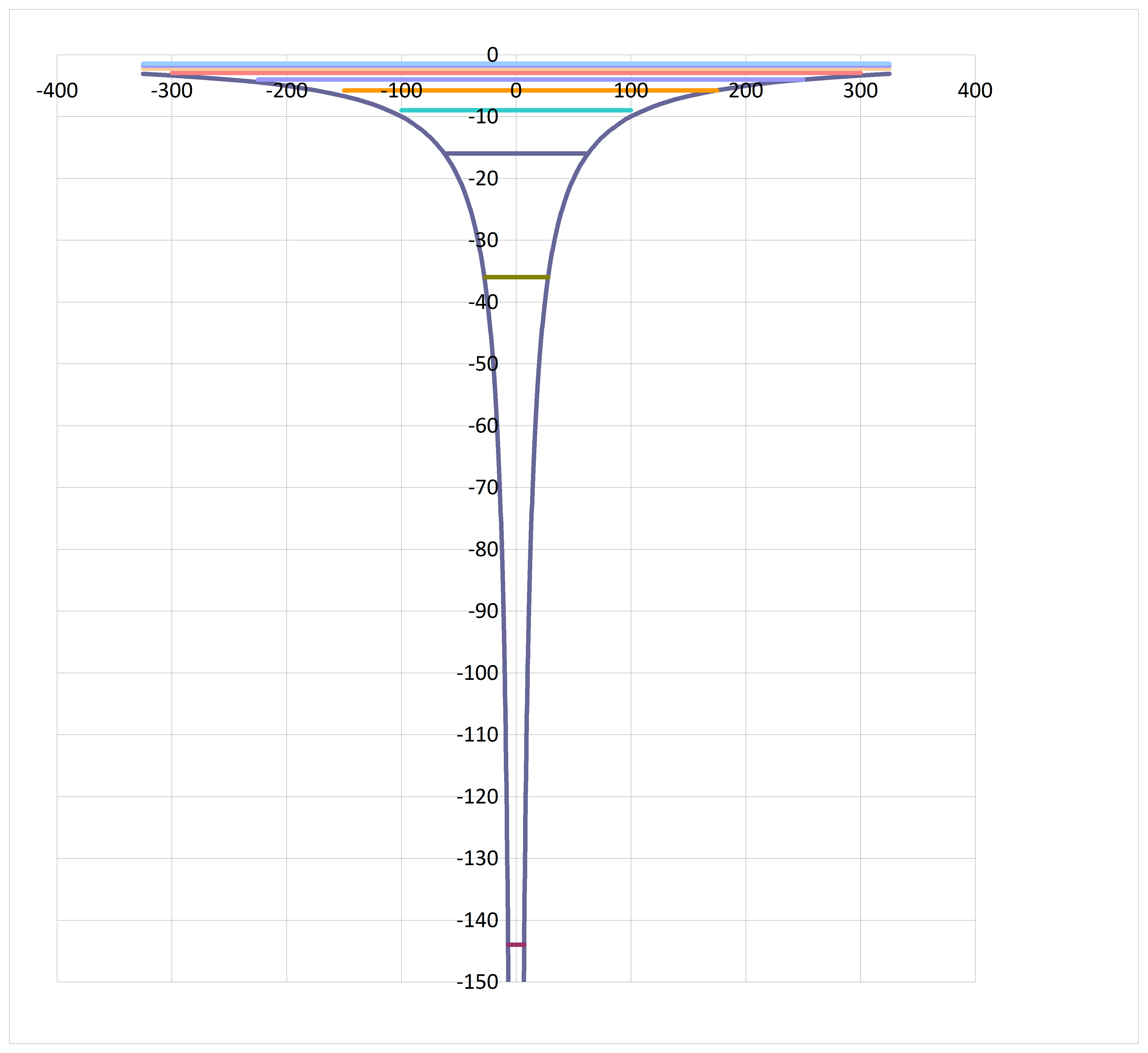
Enkele eigenschappen van het spectrum van het elektron in het ééndimensionale doosje, dat is geschetst in figuur 4.7, kloppen hiermee, andere eigenschappen niet.
Correcte voorspellingen van het model zijn:
- Dat er een beperkt aantal mogelijke energieniveaus is.
- De orde van grootte van de energieverschillen tussen de niveaus (Dit reken je na in onderstaande Onderzoeksopdracht).
De belangrijkste incorrecte voorspelling is:
- Het model van het deeltje in een doosje zegt dat de energieën steeds verder uit elkaar liggen, hoe hoger je komt. In werkelijkheid is dat andersom; zie extra paragraaf 4.2.
Onderzoeksopdracht
De laagste toestand is de toestand met n=1, de aangeslagen toestanden hebben hogere waarden van n.
- In de grondtoestand heeft het deeltje een energie die ongelijk is aan nul. Energie nul is niet mogelijk. Leg uit hoe dit voor een opgesloten deeltje ook uit de onbepaaldheidsrelatie van Heisenberg volgt.
- Ga aan de hand van de formule voor de energieniveaus van een deeltje in een doosje na dat hogere niveaus steeds verder uit elkaar liggen.
- Bereken de energie van een foton dat kan zorgen voor een overgang van n=1 naar n=2, voor een doosje zo groot als een waterstofatoom, waarbij je als massa van het opgesloten deeltje de massa van een elektron neemt.
- Klopt de orde van grootte van je antwoord van vraag c) met de waarneming dat atomen, ook waterstofatomen, fotonen van zichtbaar licht en van UV-straling kunnen absorberen en uitzenden?