In het ruimtetijddiagram hebben we een raster getekend van horizontale en verticale
lijnen. Bij elk van de assen van het stelsel hoort een schaal: een doorsnee
stadskaart heeft vakjes van een halve kilometer in beide richtingen, maar op een
kaart van Europa zal de eenheid eerder 100 km zijn. Wij moeten de schaal voor de
ruimte- en tijdassen dus zo kiezen dat de dingen die ons interesseren duidelijk te
onderscheiden zijn.
Bij de verschijnselen waar wij ons op gaan richten is vooral de verhouding tussen
de eenheden langs beide assen van belang: de afstand per tijd, zeg kilometer per
uur, maar dat is per definitie het begrip snelheid. We kiezen de verhouding tussen
de eenheden langs de ruimte- en de tijd-as dus met het oog op de snelheden die ertoe
doen in de speciale relativiteitstheorie. We zullen zien dat dat geen alledaagse
snelheden zijn van meters per seconde of kilometers per uur, niet de snelheid van
een wandelaar, een vliegtuig of zelfs het geluid, maar een zeer uitzonderlijke
snelheid, te weten de lichtsnelheid, die wordt aangeduid met de letter c
(van celeritas, Latijn voor snelheid).
Wat is er zo bijzonder aan de lichtsnelheid? Oorspronkelijk had niemand door dat er
iets bijzonders mee aan de hand was. Maar toen verscheen Einstein ten tonele, die
inzag dat de lichtsnelheid (in vacuüm) universeel is - een universele
natuurconstante (zie paragraaf 1.6). Tot die tijd was het gewoon een eindige
snelheid als alle andere. Rond 1850 bepaalde de Franse natuurkundige Fizeau de
grootte ervan in een eenvoudig maar slim opgezet experiment. Hij vond een snelheid
die dicht tegen de 300.000 kilometer per seconde aan lag. Sinds 21 oktober 1983 is c
zelfs precies 299.792.458 meter per seconde - omdat de meter sindsdien gedefinieerd
is aan de hand van c. Het is een enorm getal, wat verklaart dat wij de
lichtsnelheid als oneindig ervaren: als we het licht aandoen lijkt dat
ogenblikkelijk de hele kamer te vullen. Toch is dat een illusie: het licht moet van
de gloeilamp naar de muren reizen, wat gewoon tijd kost, ook al is het niet meer dan
een miljoenste van een seconde. Ook al lijkt de lichtsnelheid oneindig, ze is het
niet.
We zullen ons dus bezig houden met heel snelle bewegingen - vaak in de buurt van de
lichtsnelheid. We zetten zulke bewegingen uit in een plaats-tijddiagram. (Het is in
de relativiteitstheorie gebruik om de tijd verticaal uit te zetten. Dit heeft geen
diepere betekenis en is terug te voeren op traditie.) Om de schaal op de assen van
het plaats-tijddiagram te bepalen, gaan we uit van de seconde als de eenheid van
tijd. Een as-indeling die we in de natuurkunde gebruiken voor fietsers, auto's en
dergelijke is hier niet handig: als de tijd 1 hokje (1 seconde) verstrijkt, zou het
licht 300.000 hokjes (met elk hokje 1 km) doorlopen.
Om dit op te lossen voeren we een nieuwe eenheid in: de lichtseconde (ls)
die gelijk is aan de afstand die het licht in één seconde in vacuüm
aflegt, dus 300.000 km. Deze afstand gebruiken we als schaal langs de tijd-as,
d.w.z. we vermenigvuldigen de tijd met de lichtsnelheid en defininiëren van nu
af aan
als de coördinaat in de tijdrichting. Hierdoor is verticaal elk hokje 300.000
km groot! En ook in de ruimterichting kiezen we hokjes met lengte 300.000 km. We
nemen dus de lichtseconde als eenheid langs zowel de tijd- als de ruimte-as.
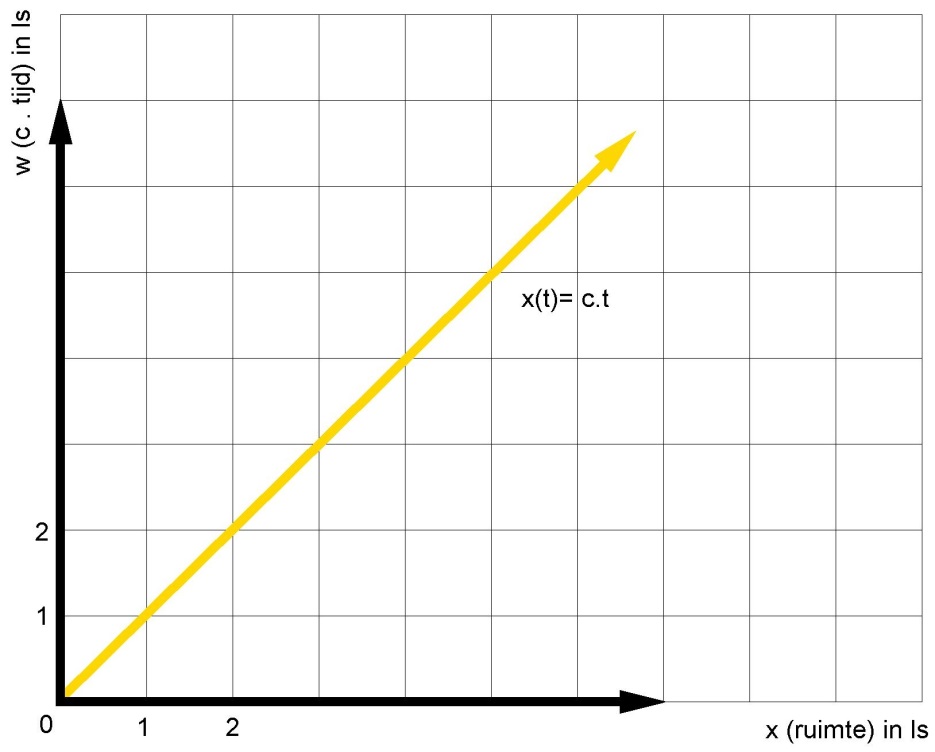
Als we nu een korte lichtflits (of nog liever: een foton, een quantum van licht)
uitzenden in de ruimterichting, legt die in ons ruimtetijd diagram een pad af dat
overeenkomt met de gele pijl in figuur 1.5. We kunnen die lijn beschrijven met de
formule
. Als t bijvoorbeeld 1 seconde is, dan zijn zowel x als w
gelijk aan c kilometer, zijnde 1 ls; als t 4,5 seconde is, is
dus 4,5 maal c kilometer,
enzovoort. Het pad van het foton maakt dus een hoek van 45o met de w-as.
Merk ook op dat een voorwerp dat zich met constante snelheid voortbeweegt,
correspondeert met een rechte lijn in het diagram, omdat het in tweemaal zoveel tijd
altijd precies een tweemaal zo grote afstand zal afleggen.