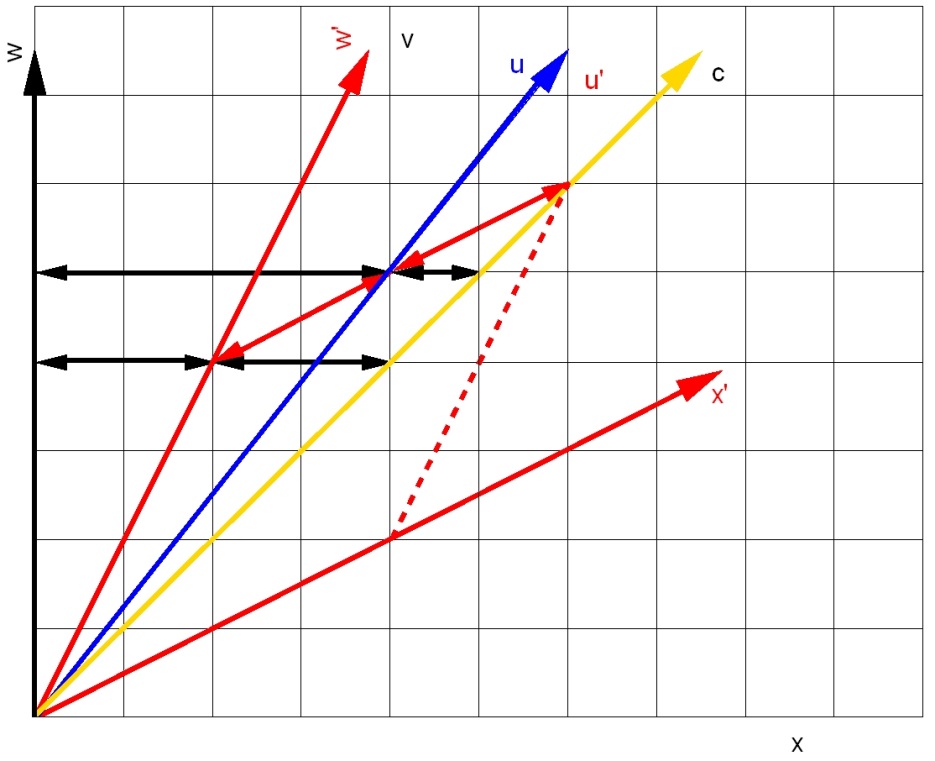
We kijken nogmaals naar een vergelijkbaar experiment, alleen heeft de trein nu
een snelheid van v = ½ c en rent het meisje met de blauwe
ogen ook met u’ = ½ c door de trein naar voren. Het is
niet moeilijk te zien waar de rode wereldlijn voor de trein in figuur 3.3 moet
lopen: omdat die half zo snel gaat als het licht, moeten de onderste twee liggende
zwarte pijlen even lang zijn. Nu weten we dat vanwege het tweede postulaat de
lichtsnelheid hetzelfde is in de rode trein als voor ons (de waarnemers in het
zwart), zodat er maar één gele pijl is die het lichtsignaal voorstelt in
beide stelsels. Maar waar moet de blauwe wereldlijn van het meisje komen?
Als iets in het rode stelsel beweegt met de helft van de lichtsnelheid, dan moet
dat voorwerp in dezelfde tijd precies half zo ver komen als een lichtsignaal in
dat stelsel. Zoals je weet worden de afstanden in de trein gemeten in de rode
x’-richting, en niet langs de horizontale zwarte lijnen. Daarom loopt de
blauwe pijl precies zo dat de twee rode tweepuntige pijlen even lang zijn, wat
betekent dat het meisje met de blauwe ogen in de x-richting inderdaad telkens de
helft van de afstand aflegt die een lichtflits in diezelfde tijd aflegt.
De vraag is nu met welke snelheid de blauwe pijl correspondeert in het zwarte
kader, dus voor de stilstaande waarnemers. Figuur 3.3 geeft ons meteen een
kwalitatief maar overduidelijk antwoord: de snelheid van de blauwe pijl is niet
½ c + ½ c = c, zoals we in al onze
naïviteit hadden verwacht, maar is duidelijk kleiner dan de lichtsnelheid.
We kunnen uit onze tekening zelfs moeiteloos begrijpen dat hoe hard het meisje in
de trein ook holt, ze voor de zwarte waarnemers nooit de snelheid c zal
bereiken zolang zij langzamer rent dan c ten opzichte van de trein! En als
ze zich wel met de lichtsnelheid zou voortbewegen, dan zou ze die snelheid ook
meteen hebben voor alle waarnemers, geheel in overeenstemming met het tweede
postulaat van Einstein.
We kunnen nog een stap verder gaan en ons afvragen wat er zal gebeuren als het
meisje een groene bal voor zich uit gooit met een snelheid kleiner dan c.
Precies dezelfde redenering als hiervoor levert dan wederom de conclusie op dat de
snelheid van de bal voor de zwarte waarnemers altijd minder zal zijn dan c.
Deze analyse leidt tot de verrassende conclusie dat je zoveel snelheden bij
elkaar kunt optellen als je maar wilt, maar als elk van die snelheden kleiner is
dan c, dan is het eindresultaat ook altijd kleiner dan c.
Met andere woorden: volgens de relativiteitstheorie is er een
maximumsnelheid voor bewegende voorwerpen, en dat is de lichtsnelheid. Deze
snelheid is absoluut in die zin dat ze hetzelfde is voor alle waarnemers.
Dit is vrij eenvoudig aan te tonen, zoals we gezien hebben, maar het blijft een
van de verrassendste en meest tegenintuïtieve gevolgen van Einsteins
postulaten. Als je je een deeltje voorstelt dat voortraast met een snelheid die
net iets kleiner is dan de lichtsnelheid, zou je toch verwachten dat je het met
een extra duwtje een snelheid zou kunnen geven die groter is dan de lichtsnelheid
... Maar nee, dat is onmogelijk; we zullen op deze kwestie terugkomen in hoofdstuk
6.
Terug naar het meisje met de blauwe ogen in de trein. De vraag was wat haar
snelheid in het zwarte stelsel is. Daar kunnen we achter komen door te kijken naar
de horizontale zwarte pijlen die aan weerszijden van de blauwe wereldlijn liggen.
We zien dan dat haar snelheid 4/5 c is. De
relativistische wet die de optelling van snelheden vastlegt, luidt voor dit geval
dus:
Dit resultaat onderstreept het feit dat deze natuurkundige manier van optellen
die we hier aangeven met <+>, niet de gewone rekenkundige optelling is, die
we aangeven met +.