3.4 Een magistrale formule

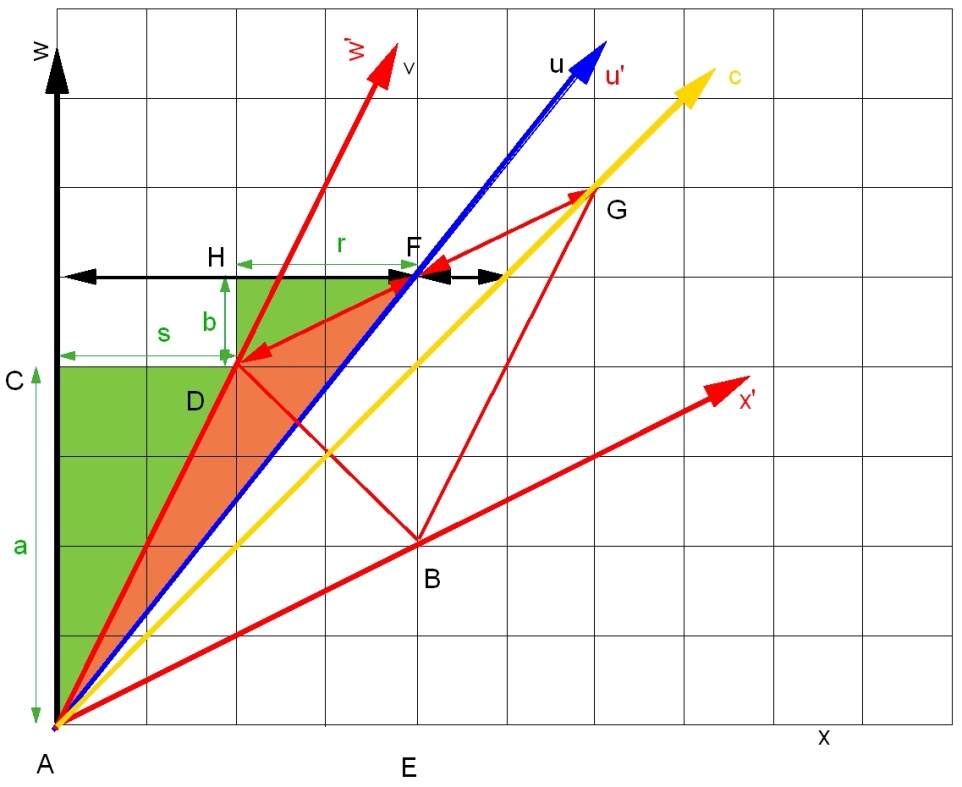
In deze paragraaf gaan we een exact kwantitatief antwoord geven op de vraag: ‘Als een rode trein langs een perron rijdt met snelheid v, en in de trein holt een meisje met blauwe ogen in de rijrichting met snelheid u’, wat is dan de snelheid u van het meisje ten opzichte van het perron?’

Om het antwoord te vinden maken we gebruik van de eigenschappen van gelijkvormige driehoeken in het platte vlak. Zie fig. 3.5. We leiden de gewenste uitdrukking voor u in termen van u’ en v, af in zeven stappen, waarbij we gebruik maken van het feit dat de twee groene driehoeken in figuur 3.5 gelijkvormig zijn: ze verschillen in grootte, maar hebben dezelfde vorm. Er is dan een vaste verhouding tussen de corresponderende zijden van beide driehoeken. Ben je klaar voor een klein potje rekenen?

Afbeelding — Figuur 3.5 Afleiding van de optelformule

In het zwarte stelsel wordt een lichtflits naar rechts uitgezonden. In 6 zwarte tijdseenheden (dit aantal is zo gekozen dat figuur 3.5 er prettig uit komt te zien) is de flits van het ruimtetijdpunt A naar het ruimtetijdpunt G gegaan. Hoe ver is de flits in het rode stelsel gekomen? In ruimtetijdpunten uitgedrukt: ook van A naar G. In tijdsduur uitgedrukt: van A naar D en in ruimte uitgedrukt: van A naar B.

De hardloopster loopt met snelheid ½ c ten opzichte van de trein. Zij komt dus in de tijdsduur AD half zo ver (gemeten ten opzichte van de trein) als het licht.
Alle tijdstippen die dezelfde tijd aangeven in de trein als het tijdstip D liggen op de lijn door DG. De halve afstand AB is gelijk aan DF. Daarom gaat de wereldlijn van de hardloopster door A en F: het is de blauwe lijn.

De twee rechthoekige groene driehoeken zijn gelijkvormig, omdat je de ene over kunt voeren in de andere door er twee eenvoudige bewerkingen op toe te passen. Eerst spiegel je de driehoek ten opzichte van een lijn die loodrecht op de gele lijn staat en door het raakpunt van de drie driehoeken loopt, en vervolgens herschaal je hem. Of anders: DF is evenwijdig aan AB en maakt daarom dezelfde hoek met de zwarte x-as als AB:

∠

DFH =

∠

EAB. De rode assen w’ en x’ maken gelijke hoeken met de zwarte assen w en x, dus

∠

DFH =

∠

CAD. De groene driehoeken hebben ook nog beide een rechte hoek: ze zijn gelijkvormig.

De verhouding tussen de twee loodrechte zijden van de grote driehoek, s/a, is de afstand

s = v \cdot t

die de rode trein aflegt in een bepaalde tijd, gedeeld door de afstand

a = c \cdot t

die het gele lichtsignaal aflegt in diezelfde tijd. Deze verhouding is dus gelijk aan v/c ofwel β en hangt niet af van het gekozen tijdstip.

Omdat de verhouding tussen de corresponderende zijden van beide groene driehoeken telkens hetzelfde is, geldt dat r/a = b/s. Om deze verhouding te bepalen vergelijken we hun langste zijden, die ook deel uitmaken van de rode driehoek. Vanuit het rode stelsel bezien is de verhouding tussen de kortste (DF) en de langste (AD) van deze twee rode zijden per definitie gelijk aan u’/c. Dit volgt uit precies hetzelfde argument als we bij stap 2 hebben gebruikt, maar dan voor het rode stelsel. AD staat voor de afstand die het licht heeft afgelegd in het rode kader en is even lang als DG. DF is de afstand die het meisje in dezelfde tijd heeft afgelegd in de trein. We krijgen:

\frac{DF}{AD} = \frac{u' \cdot t}{c \cdot t} = \frac{u'}{c}

Dus geldt dat b/s = u’/c en dus ook r/a = u’/c. Als we nu beide kanten van deze vergelijkingen vermenigvuldigen met respectievelijk s en a, vinden we:

b = \frac{u' \cdot s}{c} en r = \frac{u' \cdot a}{c}

De snelheid u die we willen bepalen voldoet aan een eenvoudige relatie in het zwarte kader: s+r is de afstand die het meisje heeft afgelegd in de tijdsduur (a+b)/c. De deling door c is nodig, omdat we de verticale as een ruimte-as is die we gedefinieerd hebben als c · t. Dus geldt dat

\frac{u}{c} = \frac{s + r}{a + b}

We zijn er bijna! In de vergelijking uit stap 6 vullen we de uitdrukkingen in voor b en r uit stap 5. Verder is:

a = c \cdot t en
                         s = v \cdot t

Dit gebruiken we in het resultaat van stap 6 om de beroemde formule te vinden die Einstein als eerste heeft afgeleid.

Na al dit meetkundige geploeter is het leuk om even stil te staan bij het resultaat om te kijken of het klopt met de eigenschappen die we in de vorige paragraaf al hadden afgeleid.

Als we de waarden uit het eerdere voorbeeld invullen, v = ½ c en u’ = ½ c, zien we dat figuur 3.5 ons niet voor de gek heeft gehouden. We krijgen inderdaad u = 4/5 c, dezelfde uitkomst die we eerder met het blote oog hadden afgelezen.
Als u’ en v allebei veel kleiner zijn dan de lichtsnelheid, zodat u’/c en v/c heel kleine waarden aannemen, verwachten we natuurlijk het vertrouwde newtoniaanse resultaat. In dat geval zal de term u’∙v/c² in de noemer zo piepklein zijn dat deze verwaarloosbaar is ten opzichte van de 1 ernaast. Daarom mogen we die term weglaten, zodat we de bekende formule terugkrijgen die we bij Newton zouden verwachten: u = u’ + v.
Als we voor u’ de waarde c kiezen, dan volgt uit de formule dat u = c, onafhankelijk van de waarde van v. Dit is niets anders dan de uitspraak dat de lichtsnelheid hetzelfde is voor alle waarnemers. Zelfs als je tweemaal c bij elkaar optelt, kom je uit op u = c.

Waarom kun je bij Newton snelheden gewoon bij elkaar optellen, terwijl daar bij Einstein zo’n ingewikkelde formule voor nodig is? Dat komt eigenlijk doordat een snelheid per definitie een ruimtelijke afstand (Δx) is, gedeeld door de verstreken tijd (Δt). Bij Newton was de tijd universeel, zodat Δt niet verandert en alleen Δx anders wordt als je overgaat van het ene naar het andere stelsel. In de theorie van Einstein daarentegen veranderen x en t allebei op verschillende wijze, waardoor de formule voor de optelling veel ingewikkelder en niet-lineair wordt.

Een buitenaards ruimteschip beweegt met een snelheid van 0,4 c richting de aarde. Ze vuren een raket op de aarde af met een snelheid van 0,8 c.

Bereken met Einsteins formule de snelheid van de raket ten opzichte van de aarde.

T.18

De snelheid van het ruimteschip in het stelsel van de aarde bedraagt v = 0,4 c (dan is de positieve as zo gekozen dat die samenvalt met de richting van de snelheid van het ruimteschip). De raket beweegt met snelheid u´ = 0,8 c ten opzichte van het ruimteschip.

Dan is de snelheid van de raket ten opzichte van ons:

u =(0,8 c + 0,4 c) / (1 + 0,4 c.0,8 c/c²) = 1,2 c / 1,32 = 10/11 c.