Hoofdstuk 5. De Lorentz-transformaties en het ruimte-tijdinterval

5.3 Past de ladder in de schuur?

Afbeelding
Figuur 5.3 Past die ladder er nou wel of niet in?

    • Misschien is het je opgevallen dat ruimte en tijd in de uitdrukkingen voor de Lorentz-transformaties op volstrekt gelijke voet behandeld worden. Aangezien we het effect van de tijdsuitrekking al zijn tegengekomen, ligt het voor de hand je af te vragen of er ook een fysisch effect optreedt voor de ruimtelijke coördinaat. Dat is zowaar het geval: het wordt de FitzGerald-Lorentz-contractie genoemd.

    Om dit effect te illustreren, beschouwen we een paradox die zich voordoet als we willen weten of een ladder in een schuur past. Deze paradox betreft een situatie met een stilstaande schuur en een ladder die er met grote snelheid doorheen raast. De stilstaande waarnemer ziet een gekrompen versie van de ladder, die volgens hem precies in de schuur past. Voor de voortsnellende waarnemer die de ladder met zich meevoert, is juist de schuur gekrompen en de ladder niet, dus volgens haar past de ladder met geen mogelijkheid in de schuur. Hoe bepalen we wie er gelijk heeft? Past die ladder er nou wel of niet in?

Tijdrek en lengtekrimp

Het verband tussen de tijdsaanduiding tussen twee klokken die ten opzichte van elkaar bewegen met snelheid v wordt gegeven door:

t ′ = t γ =t⋅ 1− β 2

De lengtekrimp van een voorwerp dat beweegt met snelheid v wordt geven door

L= L ′ γ = L ′ ⋅ 1− β 2

Lengtes transformeren dus niet op dezelfde manier als de plaatscoördinaten.

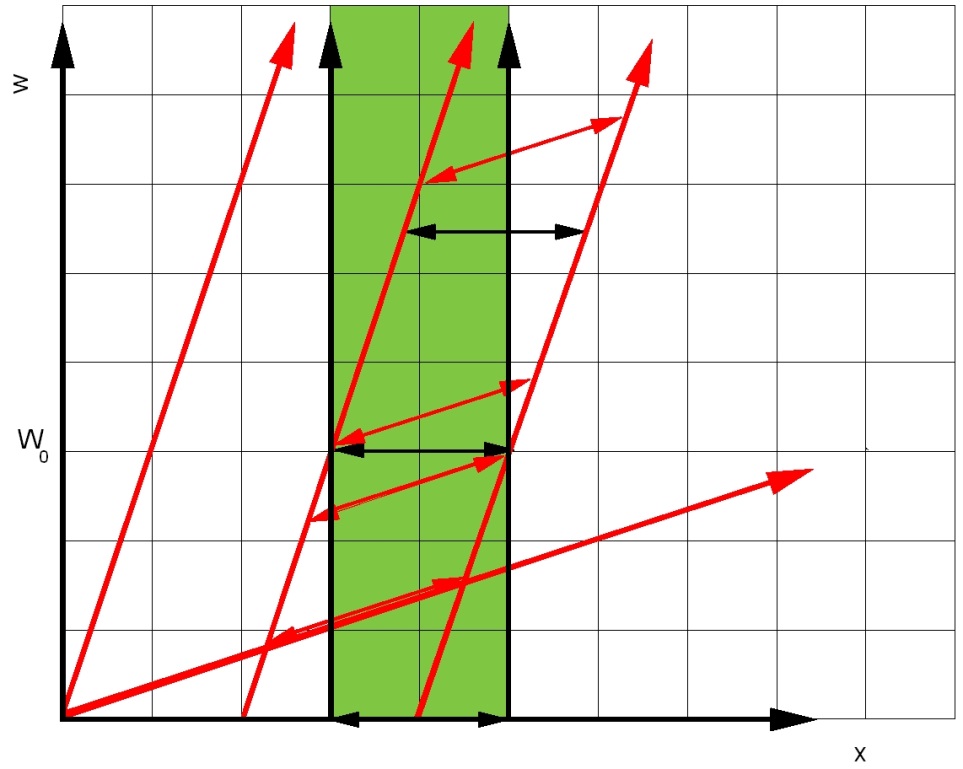
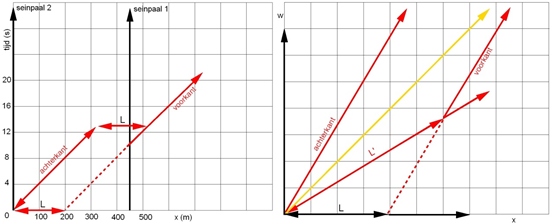
Legenda:

L is de lengte voor de meebewegende waarnemer (zwart) en L' is de lengte voor de waarnemer die beweegt ten opzichte van dat voorwerp (rood); met β= v/c de relatieve snelheidsparameter.

Het succes van de relativiteitstheorie is voor sommigen de rechtvaardiging tot het innemen van het gemakzuchtige filosofische standpunt, dat 'alles afhankelijk is van het standpunt van de waarnemer' - waarmee de door Einstein bewandelde weg eigenlijk ook al uitgezet zou zijn in het hoofd van de filosoof, met uitzondering waarschijnlijk van wat wiskundige regeltjes. Echter, niet alles is relatief - ook niet bij Einstein. Als je goed kijkt heeft Einstein slechts één gedurfde verschuiving aangebracht - wel met vergaande consequenties. Bij Newton was de tijd absoluut en de lichtsnelheid relatief, bij Einstein is dat net andersom. Met als gevolg dat, terwijl in de Newtonse mechanica tijd en lengte beide absolute grootheden zijn, bij Einstein die van de bewegingstoestand van de waarnemer af hangen.

Welk van beide inzichten, dat van Newton of dat van Einstein, de voorkeur verdient, wordt vervolgens niet door filosoferen bepaald: het zijn de uitkomsten van experimenten die dwingen het ene stelsel te verwerpen en gebruik te maken van het andere.

Je bent op weg naar Jupiter in een raket. Je neemt een liniaal mee van 30 cm. Een waarnemer op aarde zegt dat de liniaal maar 20 cm is.

  1. Hoe lang zeg jij dat de liniaal is?
  2. Welke snelheid heeft de raket?

De belangrijkste reden dat een voorwerp verkort wordt waargenomen in een stelsel waarin het voorwerp beweegt, in vergelijking met het ruststelsel is dat ....

  1. als een voorwerp met relativistische snelheid beweegt er een kracht werkt die het voorwerp samendrukt;
  2. gebeurtenissen niet in ieder stelsel gelijktijdig zijn;
  3. de liniaal die in het bewegende stelsel wordt gebruikt lengtekrimp ondervindt;
  4. de klokken in het bewegende stelsel trager lopen.