5.5 Het ruimtetijdinterval

De coördinatenstelsels waarmee we werken in onze figuren verschillen zoals je hebt gezien in twee belangrijke opzichten van elkaar. Ten eerste is er het zwarte ruststelsel waarin de assen loodrecht op elkaar staan, terwijl de assen van elk ander stelsel niet loodrecht staan maar wel gelijke hoeken maken met die van het ruststelsel. Ten tweede moeten de eenheden langs de schuine assen worden herschaald, en wel met de relativistische snelheidsfactor γ

γ = \frac{1}{\sqrt{1 - β^{2}}}

Laten we nu de verzameling waarnemers beschouwen die op het tijdstip nul met verschillende snelheden door de oorsprong komen. We vragen ze allemaal om op hun wereldlijn het punt (de gebeurtenis) te markeren waarop er op hun klok een tijdsduur van s eenheden is verstreken. Hoe ziet de verzameling gebeurtenissen die we zo vinden eruit in een ruimtetijddiagram?

De formule voor de uitrekking van de tijd leert ons dat

{(w^{'})}^{2} = (1 - β^{2}) \cdot w^{2}

en als we nu w'= s kiezen, krijgen we

(1 - β^{2}) \cdot w^{2} = w^{2} - {(β w)}^{2} = s^{2}

Gezien vanuit het ruststelsel wordt de afstand x die elke bewegende waarnemer vanuit de oorsprong heeft afgelegd, weergegeven door

x = v \cdot t = \frac{v \cdot w}{c} = β \cdot w

Zo komen we uit op een verrassend eenvoudige formule voor de verzameling punten waarin de tijd voor elke waarnemer s is, die een kromme beschrijft in het (x,w)-vlak:

w^{2} - x^{2} = s^{2}

Hoe ziet deze kromme eruit? Misschien komt de vergelijking je bekend voor met een plus- in plaats van een minteken. In dat geval zou ze een cirkel beschrijven met straal s en het middelpunt in de oorsprong. Nu er een minteken staat, wordt het geen cirkel, maar een andere befaamde wiskundige kromme: een hyperbool. Net zoals de straal een cirkel karakteriseert, wordt onze hyperbool getypeerd door zijn snijpunt met de w-as, het getal s. We kunnen simpelweg verschillende waarden voor x invullen in de formule, uitrekenen wat de bijbehorende w-waarden zijn en de punten uitzetten in het ruimtetijddiagram. 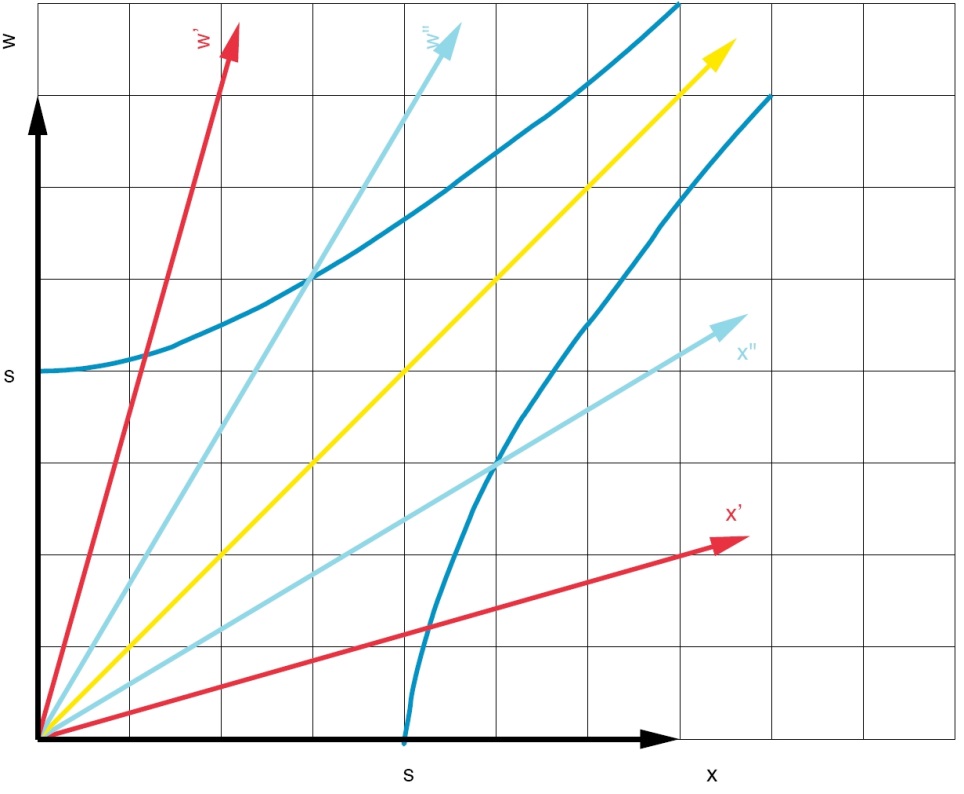Door de punten met elkaar te verbinden, vinden we krommen zoals de donkerblauwe lijn in figuur 5.8.

De 'horizontale' hyperbool wordt gekarakteriseerd door s = 4 en snijdt de zwarte, rode en lichtblauwe w-assen op de punten waar respectievelijk w = 4, w' = 4 en w'' = 4. We kunnen eenzelfde truc uithalen met meetlatten. Als we al onze waarnemers op hun wereldlijn laten aangeven waar voor hen x' = s op het tijdstip nul, komen we uit op dezelfde formule, maar dan met x en w verwisseld. Dat kun je ook bereiken door s² te vervangen door -s² in de formule. De bijbehorende kromme is de andere blauwe hyperbool in de figuur, die de x-as snijdt in het punt s.

Deze twee hyperbolen worden wel de ruimteachtige en de tijdachtige hyperbool genoemd. Dan is er ook nog het speciale geval voor s = 0, waarbij de hyperbolen ontaarden tot de lijnen w = +x en w = -x, de wereldlijnen van een foton dat in de positieve of negatieve x-richting beweegt. Deze lijnen vormen ook de asymptoten voor de ruimte- en tijdachtige hyperbolen: naarmate w en x veel groter worden dan s, naderen beide krommen de rechte lijnen steeds meer.

Wat is de meetkundige betekenis van deze prachtige krommen? Wat stellen ze voor? Daar kunnen we achter komen door de formules voor de Lorentz-transformaties te gebruiken. Als je in de formule voor de hyperbool de uitdrukkingen invult voor x en w in termen van w', x' en β = v/c uit de transformatieformules in paragraaf 5.1 , kom je na enig algebraïsch gemanipuleer uit op:

{w^{'}}^{2} - {x^{'}}^{2} = s^{2}

Dat is dus precies dezelfde vergelijking, maar dan voor coördinaten mét accentjes.

De kromme die hoort bij een bepaalde waarde van s blijkt invariant te zijn onder de Lorentz-transformaties! De afzonderlijke punten bewegen onder transformaties weliswaar heen en weer op de kromme, maar de totale verzameling punten, de hyperbool als geheel, verandert niet.

Wis- en natuurkundigen hebben het vaak over vectoren. Dat zijn een soort pijlen: ze hebben een grootte en een richting. In de euclidische meetkunde, dus in de ruimte zoals wij die kennen, is het kwadraat van de lengte r van een vector (x,y) gelijk aan de som van de kwadraten van de componenten ervan:

r^{2} = x^{2} + y^{2}

De lengte van een vector verandert niet als je hem roteert. Nu kunnen we voor een vector in de ruimtetijd (w,x) een vergelijkbaar lengtebegrip definiëren, het ruimtetijdinterval s, waarvan het kwadraat juist gelijk is aan het verschil van de componenten in het kwadraat.

s^{2} = w^{2} - x^{2}

Vanwege het minteken in de definitie kan het kwadraat van het interval zowel positief zijn als negatief of nul; we spreken respectievelijk van een tijdachtig interval, een ruimteachtig interval of een nulinterval. Ook als we een pijl tekenen tussen twee gebeurtenissen in de ruimtetijd kunnen we die een tijdachtige, een ruimteachtige of een nulvector noemen. De vectoren in de figuur die zijn aangeduid met x, x' en x'' zijn dus ruimteachtig, terwijl die met w, w' en w'' tijdachtig zijn.

De ruimteachtige hyperbool (die net als de tijdas de x-as snijdt) blijkt nog om een heel andere reden interessant te zijn. Je ziet dat deze hyperbool heel goed de wereldlijn zou kunnen zijn van een of andere waarnemer. Deze persoon reist niet met constante snelheid, maar met een voortdurende versnelling in de positieve x-richting.