6.3 Impulsbehoud

We willen nu bekijken hoe het zit met de wet van behoud van impuls. Eerst in de Euclidische ruimte waar die natuurlijk als gevolg van de wetten van Newton geldig is in de afwezigheid van externe krachten (zie appendix 7.3), en vervolgens naar de generalisatie daarvan in de Minkowski ruimtetijd.

We beschouwen een simpel botsingsexperiment, waarbij er van links en van rechts een deeltje met massa m en snelheid v naar elkaar toe bewegen die botsen in de oorsprong. We nemen aan dat ze inelastisch botsen en er dus een deeltje met massa M= 2m in rust (met V=0) in de oorsprong overblijft. Het stelsel waarin we dit waarnemen noemen we het ruststelsel.

Inderdaad: voor de botsing hebben we p_1,x = mv; en p_2,x = -mv dus de ruimtelijke impuls P_x^voor = p_1,x+p_2,x = 0, en ook na de botsing hebben we een ruimtelijke impuls P_x^na=MV=0. Het behoud van impuls voor de ruimtelijke component is dus geldig. Voor de tijdcomponent hebben voor de botsing: p_1,0+p_2,0 = 2mc ,en na de botsing: P₀=Mc. Vergelijking van de tijdcomponent voor en na de botsing levert dus het behoud van massa op, n.l. dat M = 2m en de totale massa´s voor en na de botsing gelijk zijn.

Je zou denken dat we nu klaar zijn en het probleem hebben opgelost, maar we moeten niet te vroeg juichen. Laten we eerst eens kijken hoe dit experiment er relativistisch in een ander, bewegend stelsel uitziet.

We kiezen een bewegende waarnemer die in het stelsel van het rechter deeltje zit (en die zich dus naar links beweegt met een snelheid –v t.o.v. het ruststelsel). Voor de bewegende waarnemer geldt dat wij ons bewegen met een snelheid +v. Om de snelheid u van het naar rechts bewegende deeltje te bepalen in het bewegende stelsel moeten wij de optelformule van snelheden toepassen (zoals besproken in par. 3.3), waar we hebben laten zien dat

u = \frac{u^{'} + v}{1 + u^{'} \cdot v / c^{2}}

Hierin is u de snelheid van het linkerdeeltje ten opzichte van de bewegende waarnemer, u’ de snelheid van het linkerdeeltje ten opzichte van het ruststelsel en v de snelheid van het ruststelsel ten opzichte van de bewegende waarnemer. In ons voorbeeld geldt bovendien dat u' = v zodat

u = \frac{2 v}{1 + v^{2} / c^{2}}

Dus voor de botsing gezien vanuit het bewegende stelsel hebben we:

P_{x}^{voor} = p_{1, x} + p_{2, x} = 0 + m \cdot u = 2 m \cdot v / (1 + v^{2} / c^{2})

Help! We zien dat in dit stelsel P_x^voor niet gelijk is aan P_x^na! Impuls lijkt niet langer behouden! Wat is hier gaande? Impulsbehoud was geldig in het ruststelsel maar niet in het bewegende stelsel? Een schending van het relativiteitspostulaat, een natuurwet die waar is in het ene inertiaalstelsel maar niet in een andere? Merk op dat in de Newtoniaanse mechanica de optelformule voor snelheden geeft dat w = v+v = 2v en dan klopt de wet van impulsbehoud juist wel in beide stelsels.

Maar we hebben iets vergeten! In de relativiteitstheorie is de massa van een deeltje afhankelijk van de grootte van zijn snelheid, dus m(v)=γ(v)m, met γ(v) de relativistische snelheidsfactor. Voor de behoudswet van impuls in het bewegende stelsel moeten we dus schijven:

P_{x}^{voor} = m (u) \cdot u = M (v) \cdot v = P_{x}^{na}

De massa van het bewegende deeltje zoals gezien door de bewegende waarnemer is m(u) en de massa van het zware deeltje M is gelijk aan

M (v) = γ (v) \cdot M = γ (v) \cdot 2 m (v)

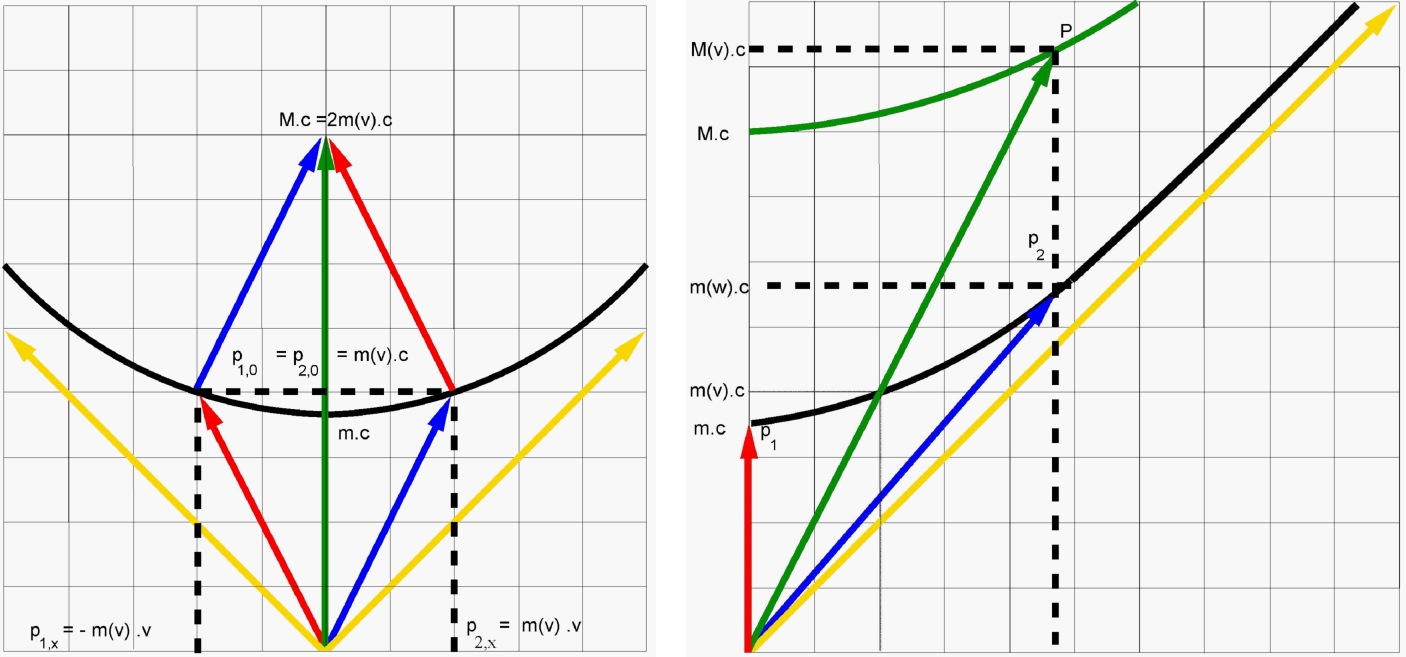
en dus niet gelijk aan 2m. De verschillende situaties voor beide stelsels zijn in de bovenstaande relativistische ruimtetijddiagrammen weergegeven:

Met een berekening kunnen we nu nagaan of inderdaad aan impulsbehoud is voldaan. We vullen in de vergelijking voor u zoals hierboven gegeven:

\begin{array}{l} P_{x}^{voor} = m (u) \cdot u = m \cdot \frac{1}{\sqrt{1 - u^{2} / c^{2}}} \cdot \frac{2 v}{1 + v^{2} / c^{2}} \\ = 2 m \cdot v \cdot \frac{1}{1 - v^{2} / c^{2}} \end{array}

Dit is inderdaad gelijk aan

P_{x}^{na} = M (v) \cdot v = 2 m \cdot v \cdot \frac{1}{1 - v^{2} / c^{2}}

Er is dus voldaan aan impulsbehoud in de relativiteitstheorie als we accepteren dat de massa afhangt van de snelheid. De massa m=m(0) van een deeltje dat stilstaat wordt wel de rustmassa genoemd.

Maar we leren uit deze exercitie ook dat in de relativiteitstheorie het behoud van rustmassa niet langer geldig is; deze behoudswet wordt vervangen door het behoud van de tijdcomponent van de impulsvector. Die vertelt ons dat de totale relativistische massa, die snelheidsafhankelijk is, behouden blijft. Voor de rode waarnemer is de vergelijking:

P_{x}^{na} = M (v) v = 2 m \cdot v \cdot \frac{1}{1 - v^{2} / c^{2}}

Net als voor de impuls kunnen we door berekening controleren dat dit inderdaad een gelijkheid is.