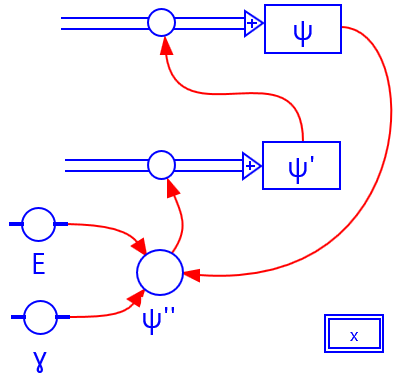
subsectie 1-dim Schrödingervergelijking

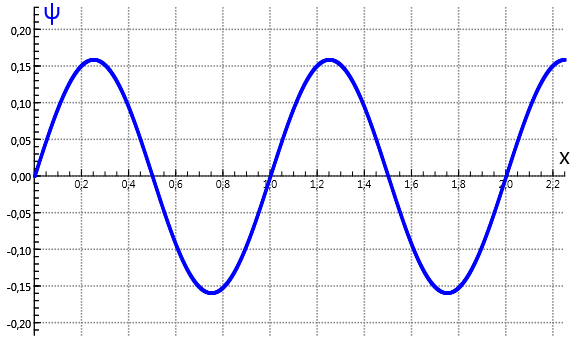
De golf die een quantumdeeltje beschrijft wordt de 'golffunctie' genoemd. In het geval van een quantumdeeltje-in-een-doosje wordt stilzwijgend aangenomen dat deze golffunctie gegeven wordt door een sinusfunctie $ψ (x) = A \cdot \sin (k \cdot x)$ met amplitude $A$ en golfgetal $k = 2 π / λ$ .

De berekening van de tweede afgeleide van deze golffunctie geeft de golfvergelijking: $\frac{d^{2} ψ (x)}{d x^{2}} = - k^{2} \cdot ψ (x)$ Invullen van de debroglie-relatie $k = (2 π / h) m \cdot v$ resulteert in de Schrödingervergelijking (1-dimensionaal, stationair) zoals hiernaast weergegeven.¹ Hierin is de totale energie $E$ de som van de kinetische energie en de potentiële energie $V (x)$ van het quantumdeeltje.

In het voorbeeld hieronder wordt een oplossing berekend voor een vrij quantumdeeltje, d.w.z. $V (x) = 0$ . In de modelregels is de coördinaat $x$ genormeerd op de debroglie-golflengte $λ_{B}$ en de energie op de kinetische energie $E_{k}$ van het quantumdeeltje.

Formules uit Binas:

\frac{d^{2} ψ (x)}{d x^{2}} + \frac{8 π^{2} \cdot m}{h^{2}} (E - V (x)) \cdot ψ (x) = 0

\begin{array}{l} E = \frac{1}{2} m \cdot v^{2} + V (x) \\ λ_{B} = h / m \cdot v \end{array}

Differentievergelijkingen:

\begin{array}{l} ψ^{″} = - γ \cdot (E - V) \cdot ψ \\ Δ ψ^{'} = ψ^{″} \cdot Δ x \\ Δ ψ = ψ^{'} \cdot Δ x \end{array}

Notatie

\begin{array}{l} ψ^{″} : = d^{2} ψ / d x^{2} = d ψ^{'} / d x \\ ψ^{'} : = d ψ / d x \\ γ : = 2 m / ℏ^{2} \\ ℏ : = h / 2 π \end{array}

Dimensieloze grootheden

\begin{array}{l} x \to λ_{B} \cdot x λ_{B} = \sqrt{2 m E_{k}} / h \\ ψ^{″} \to λ_{B}^{- 2} \cdot ψ^{″} \\ E \to E / E_{k} E_{k} = (m \cdot v^{2}) / 2 \\ γ \to λ_{B}^{2} \cdot E_{k} \cdot γ = {(2 π)}^{2} \end{array}

Modelregels

\begin{array}{l} ψ^{″} = - γ \cdot E \cdot ψ \\ ψ^{'} = ψ^{'} + ψ^{″} \cdot d x \\ ψ = ψ + ψ^{'} \cdot d x \\ x = x + d x \end{array}

Grafisch model